Two resistors of resistance and having are connected in parallel. For equivalent resistance R, the correct statement is
Let be the terminal velocity attained by the rod PQ (in the steady state). If and be the currents flowing through and in this state, then current flowing through the rod PQ is (see the circuit diagram) as shown in Fig.
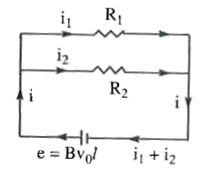
Applying Kirchoff.s loop rule, yields.
and
.....(i)
Given that, .....(ii) and .....(iii)
Also in the steady state, the acceleration of PQ = 0.
(or) .....(iv)
Multiplying both sides by , we get
(From Eq. (ii) and (iii)]
The terminal velocity is
Substituting for in Eq. (ii),
Similarly from Eg. (iii)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:AAKASH SERIESChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-IA
Explore 58 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH SERIESChapter:ELECTROMAGNETIC INDUCTIONExercise:EXERCISE-IB
Explore 18 Videos
- ELECTRIC FIELD AND POTENTIALBook:AAKASH SERIESChapter:ELECTRIC FIELD AND POTENTIALExercise:PROBLEMS (LEVEL-II)
Explore 26 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH SERIESChapter:ELECTROMAGNETIC WAVESExercise:EXERCISE -II
Explore 22 Videos
Similar Questions
Two resistor of resistance R1=(6±0.09)Ω and R2=(3±0.09)Ω are connected in parallel the equivalent resistance R with error (in Ω)
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series, (b) in parallel. Find the equivalent resistance of the (a) series combination, (b) parallel combination. Use for (a) the relation R=R1+R2 and for (b) 1R'=1R1+1R2 and ΔR'R'2=ΔR1R21+ΔR2R22
View Solution
Knowledge Check
Two resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
A(800±1)ΩB(800±7)ΩC(200±7)ΩD(200±1)ΩTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
Two resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistances R1=100±3 ohm and R2=200±4 ohm are connected (a) in series , (b) in parrallel. Find the equivalent resistance of the (a) series combination , (b) parallel combination . Use for (a) the relation R=R1+R2and for (b) 1R=1R1+1R2andΔR'R,2=ΔR1R21+ΔR2R22
View SolutionTwo resistors of resistance R1=2ΩandR2=1Ω are connected in parallel with a current source of 3 A. Draw the arrangement and deduce the current I1 in R1andI2 in R2.
View SolutionTwo resistors of resistance R1=2ΩandR2=1Ω are connected in parallel with a current source of 3 A. Draw the arrangement and deduce the current I1 in R1andI2 in R2.
View Solution