If the flux of magnetic induction through each turn of a coil of resistance R and having N turns changes from ϕ1 to ϕ2 then the magnitude of the charge that passes through the coil is
ϕ2−ϕ1R
N(ϕ2−ϕ1)R
ϕ2−ϕ1NR
NRϕ2−ϕ1
The correct Answer is:B
To find the magnitude of the charge that passes through a coil of resistance R with N turns when the magnetic flux changes from ϕ1 to ϕ2, we can follow these steps:
Step 1: Understand Faraday's Law of Electromagnetic Induction
According to Faraday's law, the electromotive force (emf, E) induced in a coil is equal to the negative rate of change of magnetic flux through the coil. Mathematically, it is expressed as:
E=−NdΦdt
where N is the number of turns and Φ is the magnetic flux.
Step 2: Calculate the Change in Flux
The change in magnetic flux ΔΦ through the coil is given by:
ΔΦ=Φ2−Φ1
Step 3: Relate emf to Current and Resistance
Using Ohm's law, we know that the current I flowing through the coil is related to the emf and the resistance R by:
E=IR
From this, we can express the current as:
I=ER
Step 4: Substitute emf in Terms of Change in Flux
Substituting the expression for emf from Faraday's law into the equation for current gives:
I=NdΦdtR
Step 5: Relate Charge to Current
The charge Q that passes through the coil in a time interval Δt can be expressed as:
Q=IΔt
Substituting the expression for I into this equation gives:
Q=(NΔΦR)Δt
Step 6: Final Expression for Charge
Since ΔΦ=Φ2−Φ1, we can write:
Q=N(Φ2−Φ1)RΔt
Conclusion
Thus, the magnitude of the charge that passes through the coil is:
Q=N(Φ2−Φ1)RΔt
According to Faraday's law, the electromotive force (emf, E) induced in a coil is equal to the negative rate of change of magnetic flux through the coil. Mathematically, it is expressed as:
E=−NdΦdt
where N is the number of turns and Φ is the magnetic flux.
The change in magnetic flux ΔΦ through the coil is given by:
ΔΦ=Φ2−Φ1
Using Ohm's law, we know that the current I flowing through the coil is related to the emf and the resistance R by:
E=IR
From this, we can express the current as:
I=ER
Substituting the expression for emf from Faraday's law into the equation for current gives:
I=NdΦdtR
The charge Q that passes through the coil in a time interval Δt can be expressed as:
Q=IΔt
Substituting the expression for I into this equation gives:
Q=(NΔΦR)Δt
Since ΔΦ=Φ2−Φ1, we can write:
Q=N(Φ2−Φ1)RΔt
Thus, the magnitude of the charge that passes through the coil is:
Q=N(Φ2−Φ1)RΔt
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-IB18videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE-II32videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Additional Exercise11videos
ELECTROMAGNETIC INDUCTION
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II22videos
ELECTROMAGNETIC WAVES
Similar Questions
Magnetic flux in a circuite containing a coil of resistance 2Ωchange from 2.0Wb to 10Wb in 0.2sec. The charge passed through the coil in this time is
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
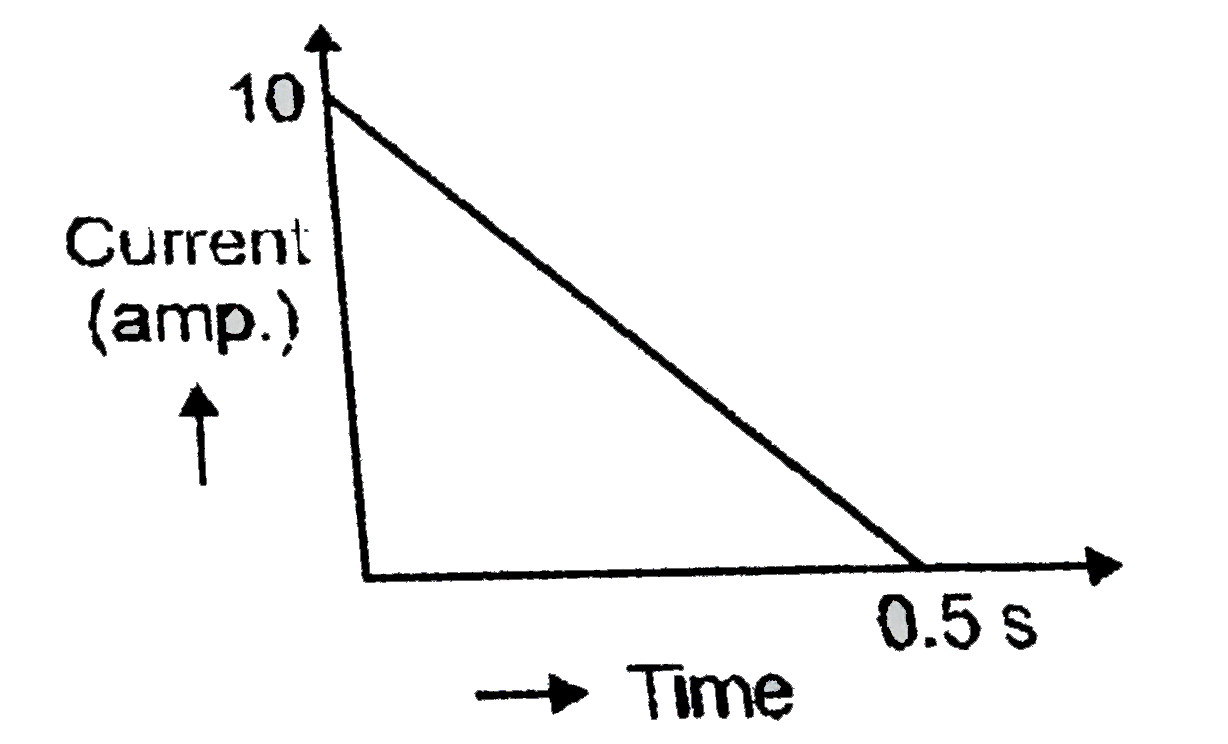 View Solution
View SolutionA resistance coil is held horizontally and a magnet is allowed to fall vertically through it . Then the acceleration of the magnet while passing through the coil is
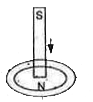 View Solution
View SolutionThe magnetic flux through a coil perpendicular to its plane is varying according to the relation ϕB=(5t3+4t2+2t−5) weber. Calculate the induced current through the coil at t = 2 second. The resistance of the coil is 5 Ω.
View SolutionSome magnetic flux is changed from a coil resistance 10Ω. As a result an induced current developed in it which varies with time as shown figure, The magnitude of changes f in flux through the coil (in webers) is
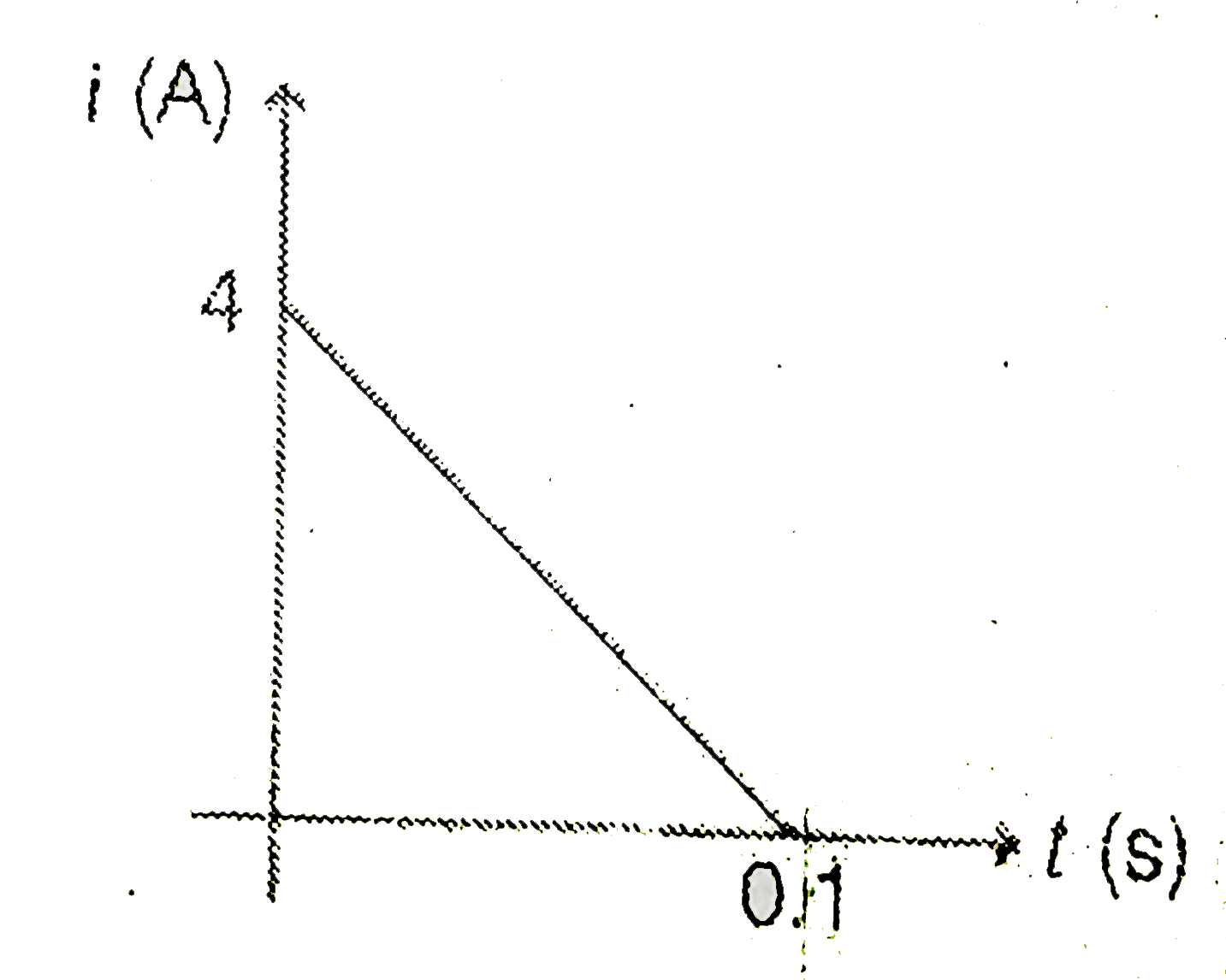 View Solution
View SolutionSome magnetic flux is changed from a coil resistance 10Ω. As a result an induced current developed in it. Which varies with time as shown figure, The magnitude of changes f in flux through the coil (in webers) is
 View Solution
View SolutionA 2A current is flowing through a circular coil of radius 10 cm containing 100 turns. Find the magnetic flux density at the centre of the coil.
View SolutionSome magnetic flux is changed from a coil of resitance 10Ω. As a result, an induced current is developed it, which varies with time as shown in Fig. 3.213. Find the magnitude of the change in flux through ythe coil in weber.
 View Solution
View SolutionThe magnetic flux through a coil perpendicular to its plane is varying according to the relation ϕB=(5t3+4t2+2t−5) weber. Calculate the induced current through the coil at t = 2 second. The resistance of the coil is 5Ω
View SolutionThe magnetic flux linked with a coil, in webers is given by the equation ϕ=3t2+4t+9. Then, the magnitude of induced emf at t = 2 s
View Solution

