−10μC,40μC and q are the charges on three identical conductors P,Q and R respectively, Now P and Q attract each other with a force F when they are separated by a distance d. Now P and Q are made in contact with each other and then separated . Again Q and R are touched and they are separated by a distance 'd' . The repulsive force between Q and R is 4F . Then the charge q is:
10μC
30μC
40μC
65μC
The correct Answer is:D
To solve the problem step by step, we will analyze the forces acting on the charges and apply the principles of electrostatics.
Step 1: Understand the Initial Attraction between P and Q
Given:
- Charge on P, qP=−10μC
- Charge on Q, qQ=40μC
The force F between P and Q when they are separated by a distance d can be expressed using Coulomb's Law:
F=k|qP⋅qQ|d2
Substituting the values:
F=k|−10⋅40|d2=k400d2
Step 2: Contact and Separation of P and Q
When P and Q are brought into contact, the total charge is shared equally because they are identical conductors. The total charge before contact is:
qtotal=qP+qQ=−10μC+40μC=30μC
After contact, each conductor will have:
qP,Q=qtotal2=30μC2=15μC
So, after separation:
- Charge on P, q′P=15μC
- Charge on Q, q′Q=15μC
Step 3: Analyze the Repulsion between Q and R
Now, Q (with charge 15μC) is brought into contact with R (with charge q). After contact, the total charge on Q and R will be:
qtotal,QR=q′Q+q=15μC+q
After contact, the charge on both Q and R will be:
qQ,R=qtotal,QR2=15+q2
Step 4: Calculate the Repulsive Force between Q and R
The repulsive force between Q and R when separated by distance d is given as 4F:
4F=k(qQ,R)2d2
Substituting qQ,R:
4F=k(15+q2)2d2
From Step 1, we know:
F=k400d2
Thus:
4F=4⋅k400d2=k1600d2
Setting the two expressions for 4F equal gives:
k1600d2=k(15+q2)2d2
Canceling k and d2 (since they are non-zero), we have:
1600=(15+q2)2
Step 5: Solve for q
Taking the square root of both sides:
40=15+q2
Multiplying by 2:
80=15+q
Thus:
q=80−15=65μC
Final Answer
The charge q is:
65μC
Given:
- Charge on P, qP=−10μC
- Charge on Q, qQ=40μC
F=k|qP⋅qQ|d2
Substituting the values:
F=k|−10⋅40|d2=k400d2
When P and Q are brought into contact, the total charge is shared equally because they are identical conductors. The total charge before contact is:
qtotal=qP+qQ=−10μC+40μC=30μC
After contact, each conductor will have:
qP,Q=qtotal2=30μC2=15μC
So, after separation:
- Charge on P, q′P=15μC
- Charge on Q, q′Q=15μC
Now, Q (with charge 15μC) is brought into contact with R (with charge q). After contact, the total charge on Q and R will be:
qtotal,QR=q′Q+q=15μC+q
After contact, the charge on both Q and R will be:
qQ,R=qtotal,QR2=15+q2
The repulsive force between Q and R when separated by distance d is given as 4F:
4F=k(qQ,R)2d2
Substituting qQ,R:
4F=k(15+q2)2d2
From Step 1, we know:
F=k400d2
Thus:
4F=4⋅k400d2=k1600d2
Setting the two expressions for 4F equal gives:
k1600d2=k(15+q2)2d2
Canceling k and d2 (since they are non-zero), we have:
1600=(15+q2)2
Taking the square root of both sides:
40=15+q2
Multiplying by 2:
80=15+q
Thus:
q=80−15=65μC
The charge q is:
65μC
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - I) (LEVEL - II (ADVANCED ) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)1videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - LECTURE SHEET (EXERCISE - I) (LEVEL - II (ADANCED) INTEGER TYPE QUESTIONS)3videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)5videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE13videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.
 View Solution
View SolutionTwo identical small conducting spheres having unequal positive charges q1 and q2 are separated by a distance r. If they are now made to touch each other and then separated again to the same distance, the electrostatic force between them in this case will be
View SolutionTwo identical small conducting spheres having unequal positive charges q1 and q2 are separated by a distance r. If they are now made to touch each other and then separated again to the same distance, the electrostatic force between them in this case will be
View SolutionConsider three charged bodies P,Q and R. If P and Q repel each other and P attracts R, what is the nature of force between Q and R ?
View SolutionTwo identical conducting balls A and B have charges- Q and + 3Q respectively. They are brought in contact with each other and then separated by a distance d part. Find the nature of the Coulomb force between them.
View SolutionTwo point charges separated by a distance d repel each other with a force of 9N. If the separation between them becomes 3d, the force of repulsion will be
View SolutionTwo identical metal spheres having charges +q and +q respectively. When they are separated by distance r, exerts force of repulsion F on each other. The spheres are allowed to touch and then moved back to same separation. The new force of repulsion will be
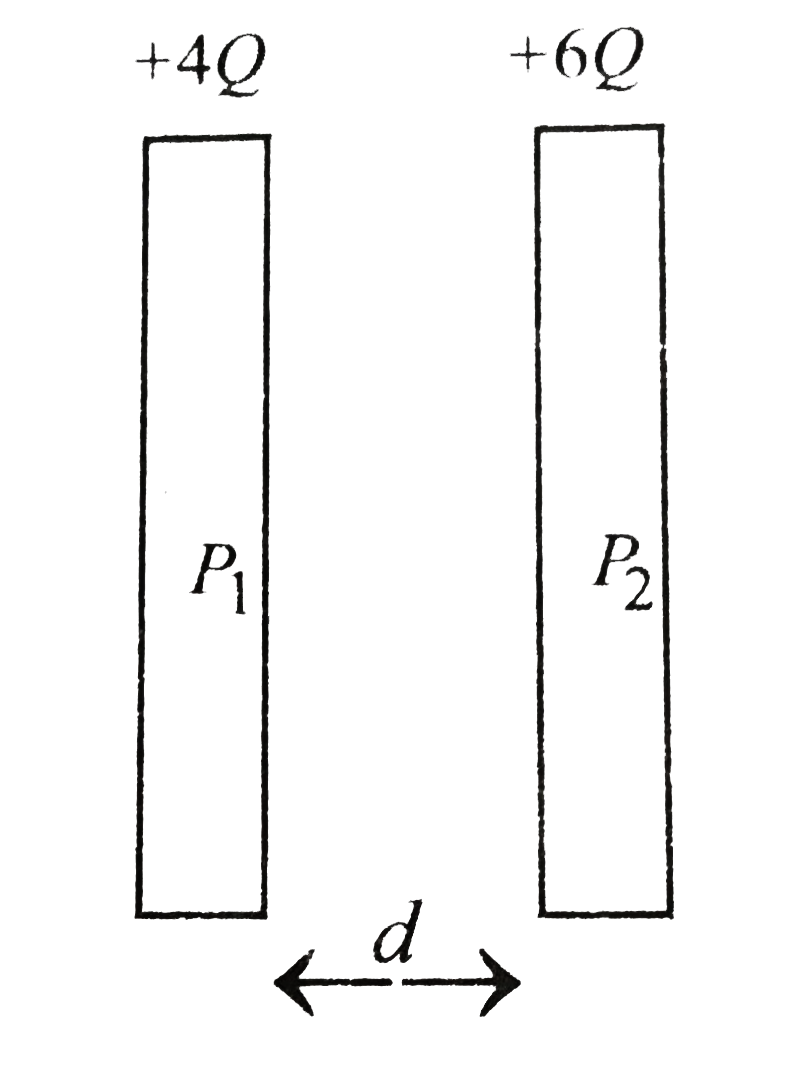
View SolutionTwo identical conducting very large plates P1andP2 having charges +4Qand+6Q are placed very closed to each other at separation d. The plate area of either face of the plate is A. The potential difference between plates P1andP2 is
 View Solution
View SolutionTwo identical metals balls with charges +2Q and −Q are separated by some distance and exert a force F on each other . They are joined by a conducting wire , which is then removed. The force between them will now be
View SolutionThree forces P, Q and R are acting on a particel in the plane, the angle between P and Q and that between Q and R are 150∘ and 120∘ respectively. Then for equilibrium, forces P, Q and R are in the ratio
View Solution

