A uniformly charged and infinitely long line having a liner charge density λ is placed at a normal distance y from a point O. Consider a sphere of radius R with O as the center and Rgty. Electric flux through the surface of the sphere is

flux crossing the sphereis zero if d>R
flux crossing the sphere is 2l√R2−d2ε0ifd<R
If d>R, the magnitude of maximum potential of maximum potential difference between two points on the sphere is λ2πε0In(d+Rd−R)
When a charge is moved along any diameter of the sphere in the plane perpendicular to the wire, work done is zero.
The correct Answer is:A, B, C, D
Step by step video & image solution for A uniformly charged and infinitely long line having a liner charge density lambda is placed at a normal distance y from a point O. Consider a sphere of radius R with O as the center and Rgty. Electric flux through the surface of the sphere is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) MATRIX MATCHING TYPE QUESTIONS
1 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)
14 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
A uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is
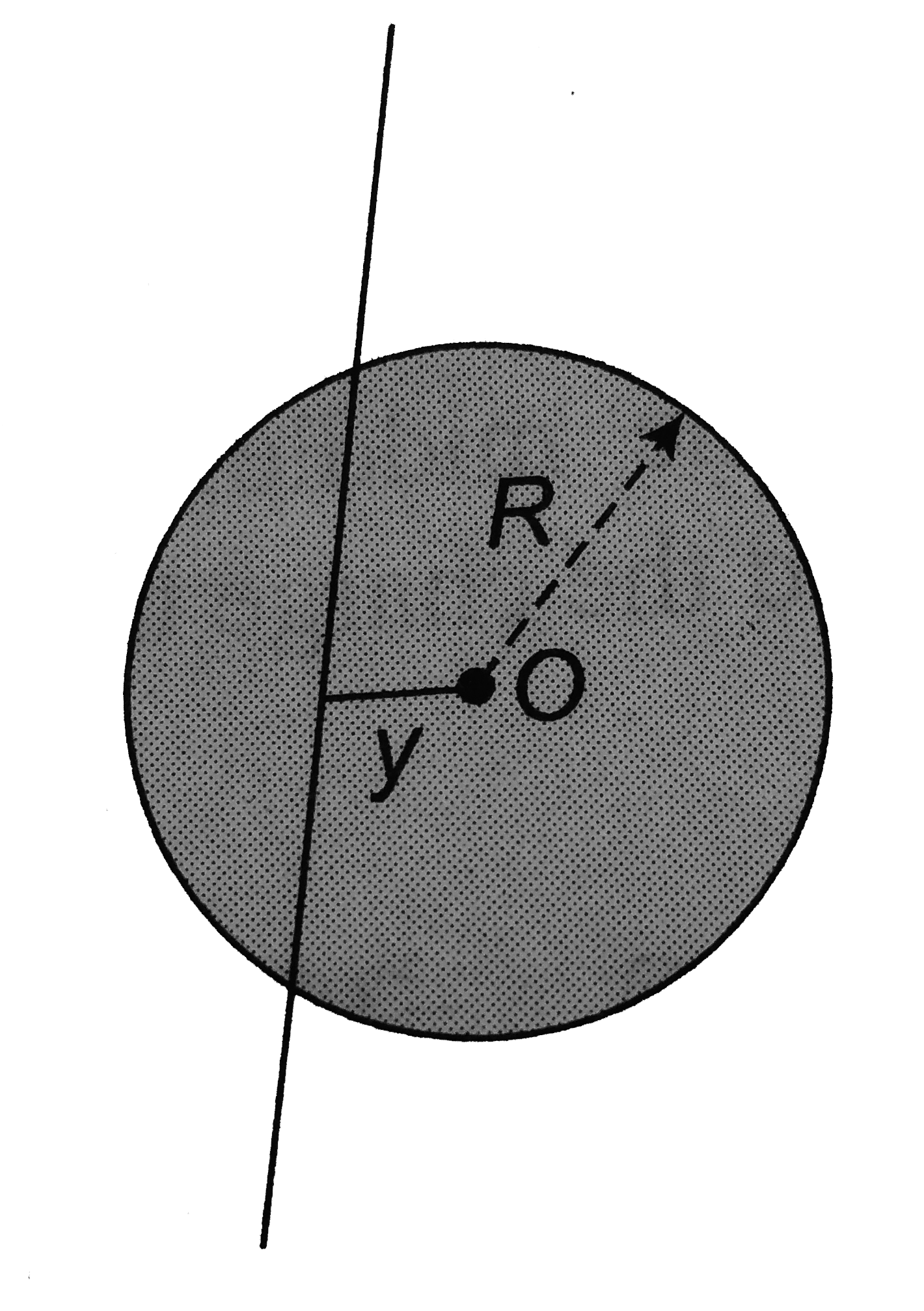
View SolutionA uniformly charged and infinitely long line having a linear charge density 'λ' is placed at a normal distance y from a point O. Consider a sphere of radius R with O as centre and R>y. Electric flux through the surface of the sphere is

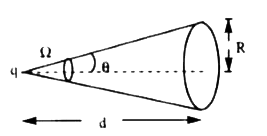
View SolutionAn infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where R<d and R>d.

View SolutionAn infinitely long line charge having a uniform charge per unit length λ lies at a distance d from a point O as shown in figure. Determine the total electric flux through through the surface of a sphere of radius R centered at O resulting from this line charge. Consider both cases where R<d and R>d.

View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
View SolutionA charge q0 is distributed uniformly on a ring of radius R. A sphere of equal radius R constructed with its centre on the circumference of the ring. Find the electric flux through the surface of the sphere.
View SolutionA charge 'Q' is placed at the centre of a hemispherical surface of radius 'R'. The flux of electric field due to charge 'Q' through the surface of hemisphere is
View SolutionA thin straight infinitely long conducting wire having charge density λ enclosed bya cylindrical surface of radius rand length lr, its axis coinciding with the length of the wire. Find the expression for the electric flux through the surface of the cylinder.
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .

View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View Solution
