Two point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.
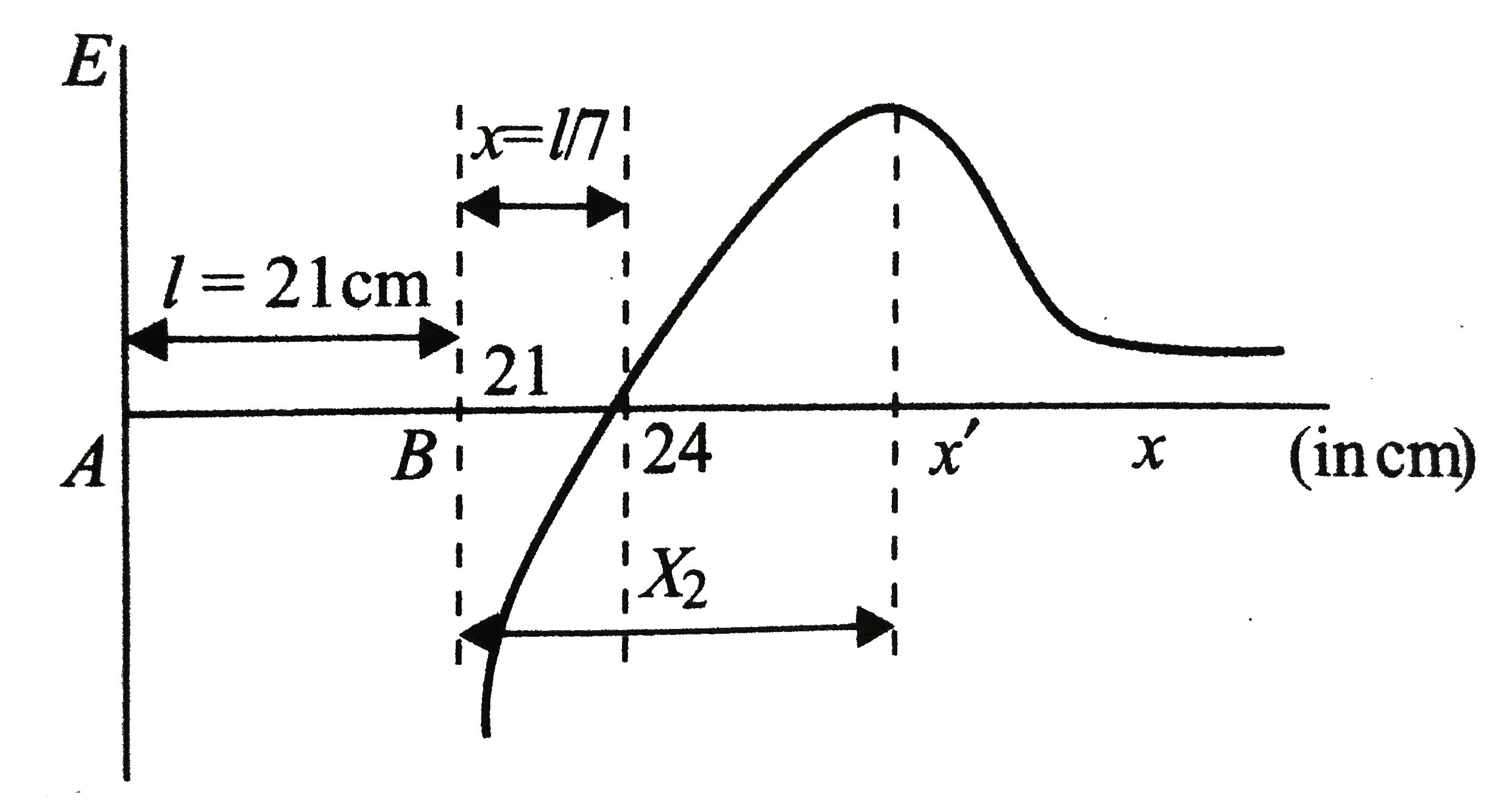
(a) Find the sign of the charges.
(b) Find the ratio between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.
Q1 is positive charge while Q2 is negative charge
The ratio of the absoulte value of the charges ∣∣∣Q1Q2∣∣∣(a+la)2
The value of b, where the field intensity is maximum is b=l(l+a2a)2/3−1
The value of b , where the filed intesity is maximum is
The correct Answer is:A, B, D
Step by step video solution for Two point charge Q_(a) and Q_(b) are positional at point A and B. The field strength to the right of charge Q_(b) on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21 cm. (a) Find the sign of the charges. (b) Find the ratio between the absolute value of charge Q_(a) and Q_(b). (c ) Find the coordinate x of the point where the field strength is maximum. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS)
2 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED)MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
20 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
Similar Questions
Two point charges Q and -Q/4 are separated by a distance x.
View SolutionThe positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
View SolutionTwo fixed charges 4Q (positive) and Q (negative) are located at A and B. the distance AB being 3 m.
View SolutionTwo point charges qA=3μCandqB=−3μC are located 20cm apart in vacuum. What is the electric field at the mid point of the line joining the two charges.
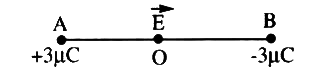
View SolutionTwo charge +aq and -q are kept apart. Then , at any point on the right bisector of line joining the two charge
View SolutionTwo point charges +Q and -Q are separated by a certain distance. The resultant electric field is parallel to the line joining the charges at the points
View SolutionTwo point charges Q and -3Q are placed at some distance apart. If the electric field at the location of Q is →E, the field at the location of - 3Q is
View SolutionTwo point charges q and −q are separated by a distance 2l. Find the flux strength vector across the circle of radius R placed with its centre coinciding with the of line joining the two charges in the perpendicular plane.
View SolutionA positive charge +q1 is located to the left of a negative charge −q2 On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if q2=−12μC , what is the value of charge q1∈μC
View SolutionTwo point charges +q and −q are placed a distance x apart. A third charge is so placed that at the three charges are in equilibrium. Then
View Solution
