A positive charge +q1 is located to the left of a negative charge −q2 On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if q2=−12μC , what is the value of charge q1∈μC
44μC
12μC
32μC
64μC
The correct Answer is:A
To solve the problem, we need to find the value of the positive charge q1 given that the negative charge q2=−12μC and the two points where the potential is zero.
1. Identify the Positions of the Charges:
- Let q1 be the positive charge located to the left of the negative charge q2.
- The distance between the negative charge q2 and the first point (where potential is zero) is 4 cm to the left of q2.
- The second point (where potential is zero) is 7 cm to the right of q2.
2. Define the Points:
- Let the position of q2 be at the origin (0 cm).
- The first point (C) is at −4cm (4 cm to the left of q2).
- The second point (D) is at +7cm (7 cm to the right of q2).
- The distance from q1 to point C is dC=4+d (where d is the distance between q1 and q2).
- The distance from q1 to point D is dD=7−d.
3. Set Up the Potential Equations:
- The electric potential V at a point due to a charge is given by:
V=kqr
- For point C:
VC=kq1dC+k−q24=0
This simplifies to:
q1d+4=q24
- For point D:
VD=kq1dD+k−q27=0
This simplifies to:
q17−d=q27
4. Substituting q2:
- Substitute q2=−12μC into both equations:
- From point C:
q1d+4=−124⟹q1d+4=−3⟹q1=−3(d+4)
- From point D:
q17−d=−127⟹q1=−12(7−d)7
5. Equate the Two Expressions for q1:
- Set the two expressions for q1 equal to each other:
−3(d+4)=−12(7−d)7
- Cross-multiply to eliminate the fraction:
−21(d+4)=−12(7−d)
- Simplify:
21d+84=84−12d
- Combine like terms:
33d=0⟹d=0
- Substitute d=0 back into either equation to find q1:
q1=−3(0+4)=−12μC
6. Final Calculation:
- Since q1 is a positive charge, we take the absolute value:
q1=12μC
Final Answer:
The value of charge q1 is 12μC.
- Let q1 be the positive charge located to the left of the negative charge q2.
- The distance between the negative charge q2 and the first point (where potential is zero) is 4 cm to the left of q2.
- The second point (where potential is zero) is 7 cm to the right of q2.
- Let the position of q2 be at the origin (0 cm).
- The first point (C) is at −4cm (4 cm to the left of q2).
- The second point (D) is at +7cm (7 cm to the right of q2).
- The distance from q1 to point C is dC=4+d (where d is the distance between q1 and q2).
- The distance from q1 to point D is dD=7−d.
- The electric potential V at a point due to a charge is given by:
V=kqr
- For point C:
VC=kq1dC+k−q24=0
This simplifies to:
q1d+4=q24
- For point D:
VD=kq1dD+k−q27=0
This simplifies to:
q17−d=q27
- Substitute q2=−12μC into both equations:
- From point C:
q1d+4=−124⟹q1d+4=−3⟹q1=−3(d+4)
- From point D:
q17−d=−127⟹q1=−12(7−d)7
- Set the two expressions for q1 equal to each other:
−3(d+4)=−12(7−d)7
- Cross-multiply to eliminate the fraction:
−21(d+4)=−12(7−d)
- Simplify:
21d+84=84−12d
- Combine like terms:
33d=0⟹d=0
- Substitute d=0 back into either equation to find q1:
q1=−3(0+4)=−12μC
- Since q1 is a positive charge, we take the absolute value:
q1=12μC
The value of charge q1 is 12μC.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A positive charge +q1 is located to the left of a negative charge −q2. On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity.The first place is between the charge and is 4.00 cm to the left of the negative charge. The second place is 7.00 cm to the right of the negative charge. If q2=−12μCandq1=11×xμC, what is the value of x.
View SolutionA charge Q is placed at the centre of the line joining two point charges +q and +q as shown in figure. The ratio of charges Q and q is
 View Solution
View SolutionCharges Q and -2Q are placed at some distance. The locus of points in the plane of the charges where the potential is zero will be :
View SolutionA positive point charge q1 is placed at (a,0) and another positive point charge q2 is placed at (0,a) . Find the force acting on q1.
View SolutionName the negatively charged and positively charged components of a nucleosome.
View SolutionTwo point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.
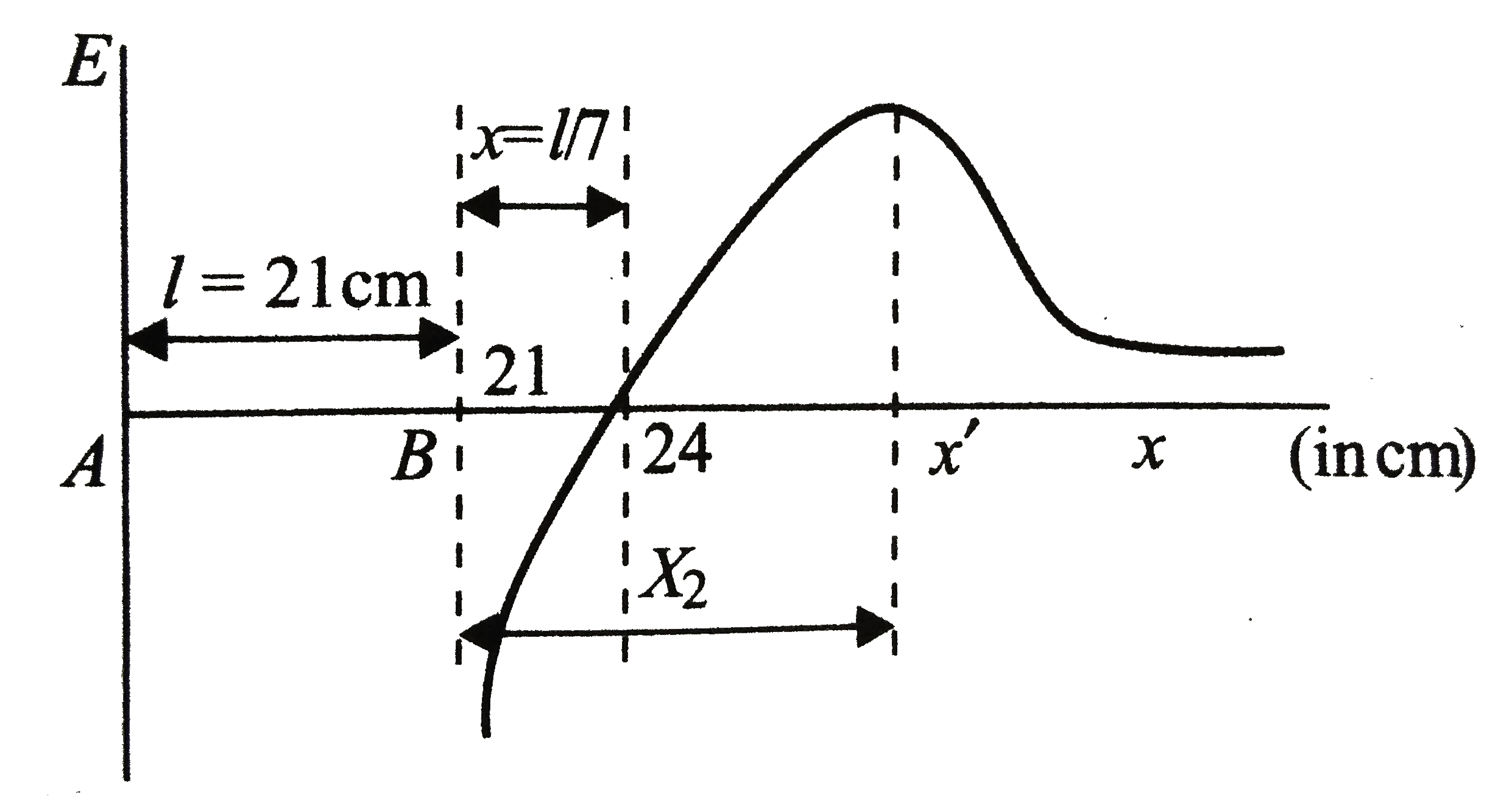
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.View SolutionTwo point charge Qa and Qb are positional at point A and B. The field strength to the right of charge Qb on the line that passes through the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincides with the positive direction of the x-axis. The distance between the charges is l=21cm.

(a) Find the sign of the charges.
(b) Find the ratio between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strength is maximum.View SolutionA charge Q is place at each of the opposite corners of a square. A charge q is placed at each of the other two corners. If the net electrical force on Q is zero, then Q/q equals:
View SolutionSuppose a charge +Q1 is given to the positive plates and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
View SolutionWhen a negatively charged body is placed in contact with the negatively charged disc of G.L.E. Its leaves ___________
View Solution

