Three capacitors with capacitances of 1μF,2μFand3μF are connected in series. Each capacitor gets punctured, if a potential difference just exceeding 100 volt is applied. If the group is connected across 220 volt circuit then the capacitor most likely to puncture first is
capacitance 1μF
capacitance 2μF
capacitance 3μF
capacitance 1μF (or) 2μF (or) 3μF
The correct Answer is:A
To solve the problem, we need to determine which capacitor is most likely to puncture first when connected in series across a 220V circuit. The capacitors have capacitances of 1μF, 2μF, and 3μF.
1. Understand Capacitors in Series:
When capacitors are connected in series, the total capacitance (C_total) can be calculated using the formula:
1Ctotal=1C1+1C2+1C3
where C1=1μF, C2=2μF, and C3=3μF.
2. Calculate Total Capacitance:
Plugging in the values:
1Ctotal=11+12+13
Finding a common denominator (6):
1Ctotal=66+36+26=116
Therefore,
Ctotal=611μF≈0.545μF
3. Calculate Charge on Each Capacitor:
The charge (Q) stored in a capacitor is given by:
Q=C⋅V
In a series connection, the charge on each capacitor is the same. The voltage across each capacitor can be found using:
Vi=QCi
where Vi is the voltage across capacitor i.
4. Calculate the Voltage Across Each Capacitor:
First, we need to find the total charge when the circuit is connected to 220V:
Q=Ctotal⋅V=(611μF)⋅220V=132011μC=120μC
Now, calculate the voltage across each capacitor:
- For C1=1μF:
V1=QC1=120μC1μF=120V
- For C2=2μF:
V2=QC2=120μC2μF=60V
- For C3=3μF:
V3=QC3=120μC3μF=40V
5. Determine Which Capacitor Punctures First:
Each capacitor can withstand a maximum voltage of just over 100V before puncturing. From our calculations:
- V1=120V (exceeds 100V)
- V2=60V (does not exceed 100V)
- V3=40V (does not exceed 100V)
Since the first capacitor (1μF) experiences a voltage of 120V, which exceeds its puncture threshold of 100V, it is the most likely to puncture first.
Conclusion:
The capacitor most likely to puncture first is the 1μF capacitor.
When capacitors are connected in series, the total capacitance (C_total) can be calculated using the formula:
1Ctotal=1C1+1C2+1C3
where C1=1μF, C2=2μF, and C3=3μF.
Plugging in the values:
1Ctotal=11+12+13
Finding a common denominator (6):
1Ctotal=66+36+26=116
Therefore,
Ctotal=611μF≈0.545μF
The charge (Q) stored in a capacitor is given by:
Q=C⋅V
In a series connection, the charge on each capacitor is the same. The voltage across each capacitor can be found using:
Vi=QCi
where Vi is the voltage across capacitor i.
First, we need to find the total charge when the circuit is connected to 220V:
Q=Ctotal⋅V=(611μF)⋅220V=132011μC=120μC
Now, calculate the voltage across each capacitor:
- For C1=1μF:
V1=QC1=120μC1μF=120V
- For C2=2μF:
V2=QC2=120μC2μF=60V
- For C3=3μF:
V3=QC3=120μC3μF=40V
Each capacitor can withstand a maximum voltage of just over 100V before puncturing. From our calculations:
- V1=120V (exceeds 100V)
- V2=60V (does not exceed 100V)
- V3=40V (does not exceed 100V)
The capacitor most likely to puncture first is the 1μF capacitor.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - II) (LEVEL - I (ADVANCED)) (Straight Objective Type Questions )3videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - II) (LEVEL - I (ADVANCED)) (More than one correct answer Type Questions )1videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - CAPACITORS EXERCISE - LECTURE SHEET (EXERCISE - I) (LEVEL - II (ADVANCED)) (Integer Type Questions)1videos
CAPACITORS
- BOOK - AAKASH SERIESCHAPTER - ATOMSEXERCISE - PRACTICE EXERCISE21videos
ATOMS
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEM EXERCISE - LECTURE SHEET (LEVEL - I) (MAIN) (EXERCISE - IV) (Straight Objective & More than one Correct Answer Type Questions)20videos
COMMUNICATION SYSTEM
Similar Questions
Three capacitors 3μF,6μF and 6μF are connected in series to source of 120 V. The potential difference in volt, across the 3μF capacitor will be
View SolutionA number of capacitors each of capacitance 1μF and each one of which get punctured if a potential difference just exceeding 500 volt is applied, are provided. Then an arrangement suitable for giving a capacitor of 2μF across which 3000 volt may be applied requires at least-
View Solution
Knowledge Check
- Question 1 - Select One
The potential difference between points A and B is
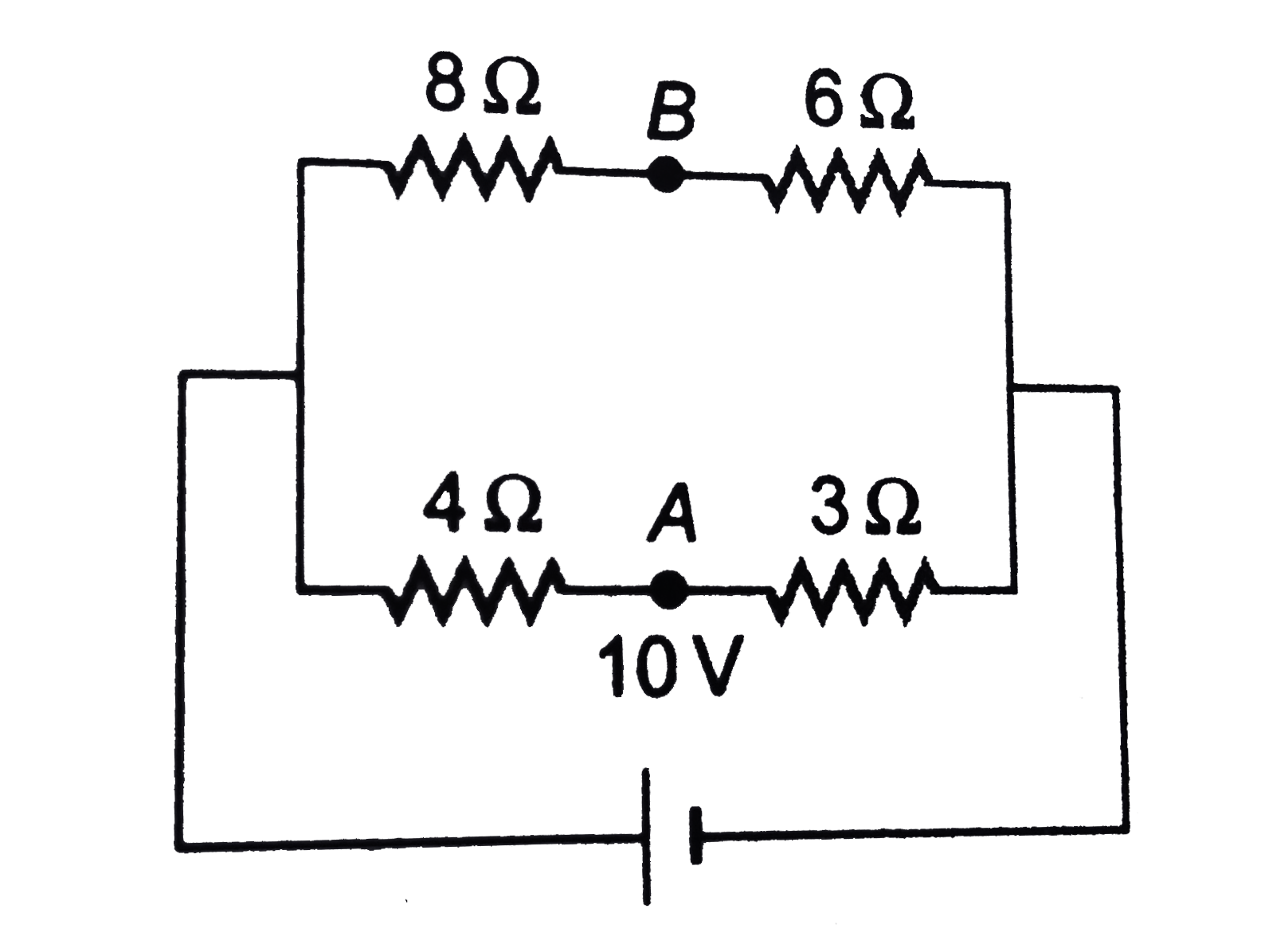 A2B5C11D18
A2B5C11D18
Three capacitors of 2μF,3μF and 6μF are joined in series and the combination is charged by means of a 24 volt battery. The potential difference between the plates of the 6μF capacitor is
View SolutionThe capacitor of capacitance 4μF and 6μF are connected in series. A potential difference of 500 volts applied to the outer plates of the two capacitor system. Then the charge on each capacitor is numerically
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
View SolutionTwo capacitors of capacitance of 6μFand12μF are connected in series with a battery. The voltage across the 6μF capacitor is 2V. Compute the total battery voltage.
View SolutionThree capacitors having capacitances of 8.4μF,8.4μF and 4.2μF are connected in series across a 36 potential difference.
(a) What is the charge on 4.2μF capacitor?
(b) What is the total energy stored in all three capacitors?
(c) The capacitors are disconnected from the potential difference without allowing them to discharge. They are then reconnected in parallel with each other, with the positively charged plates connected together. What is the voltage across each capacitor in the parallel combination?
(d) What is the total energy now stored in the capacitors?View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View Solution

