The charge flowing in a conductor varies with time as Q=at−12bt2+16ct3 where a, b and c are positive constants. If at time t, the current in the conductor is i, which of the following graphs is correct ?
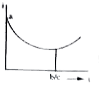


The correct Answer is:A
To solve the problem, we need to analyze the relationship between charge Q and current I as given in the equation:
Q=at−12bt2+16ct3
where a, b, and c are positive constants. The current I is defined as the rate of change of charge with respect to time:
I=dQdt
1. Differentiate the Charge Function:
To find the current I, we need to differentiate Q with respect to t:
I=dQdt=ddt(at−12bt2+16ct3)
2. Apply the Derivative:
Using basic differentiation rules:
I=a−bt+12ct2
3. Rearranging the Current Equation:
We can rearrange the equation for clarity:
I=12ct2−bt+a
4. Identify the Nature of the Graph:
The equation I=12ct2−bt+a is a quadratic equation in t. Since the coefficient of t2 (which is 12c) is positive, the graph of I versus t will be a parabola that opens upwards.
5. Find the Minimum Current:
To find the time at which the current reaches its minimum value, we need to find the vertex of the parabola. The vertex t can be found using the formula:
t=−b2a
Here, a=12c and b=−b (the linear coefficient). Thus:
t=bc
6. Conclusion:
The minimum current occurs at t=bc. Therefore, we can check the options provided in the question to identify which graph corresponds to this behavior.
To find the current I, we need to differentiate Q with respect to t:
I=dQdt=ddt(at−12bt2+16ct3)
Using basic differentiation rules:
I=a−bt+12ct2
We can rearrange the equation for clarity:
I=12ct2−bt+a
The equation I=12ct2−bt+a is a quadratic equation in t. Since the coefficient of t2 (which is 12c) is positive, the graph of I versus t will be a parabola that opens upwards.
To find the time at which the current reaches its minimum value, we need to find the vertex of the parabola. The vertex t can be found using the formula:
t=−b2a
Here, a=12c and b=−b (the linear coefficient). Thus:
t=bc
The minimum current occurs at t=bc. Therefore, we can check the options provided in the question to identify which graph corresponds to this behavior.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE-I LEVEL- II (ADVANCED) (More than one correct answer type Questions))3videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - LECTURE SHEET (EXERCISE- II LEVEL-I (MAIN) (Straight Objective Type Questions))14videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)27videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX42videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The charge flowing through a resistance R varies with time t as Q=at−bt2. The total heat produced in R is
Aa3RbBa3R2bCa3R3bDa3R6b
The charge q flowing in a conductor of uniform cross section, varies with time as q=αt−bt2. Then, the current
View SolutionA wave pulse is described by y(x,t)=ae−(bx−ct)^(2), where a,b,and c are positive constants. What is speed of this wave?
View SolutionA ardius vector of point A relative to the origin varies with time t as →r=atˆj−bt2ˆj where a and b are constants. Find the equation of point's trajectory.
View SolutionThe current in a conductor varies with time .t. as I=3t+4t2. Where I in amp and t in sec. The electric charge flows through the section of the conductor between t = 1s and t = 3s
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe linear momentum of a particle varies with time t as p=a+bt+ct2. Then, whichh of the following is correct?
View Solution

