The charge flowing in a conductor varies with times as Q=at−bt2. Then, the current
reaches a maximum and then decreases
falls to zero after t=a2b
changes at a rate of (−2b)
Both (b) and (c)
The correct Answer is:B
To solve the problem, we need to find the current flowing through a conductor when the charge Q varies with time as given by the equation:
Q=at−bt2
where a and b are constants.
Step 1: Find the expression for current I
The current I is defined as the rate of change of charge with respect to time. Mathematically, this is expressed as:
I=dQdt
Step 2: Differentiate the charge equation
Now, we differentiate the expression for Q:
I=ddt(at−bt2)
Using the rules of differentiation:
I=a−2bt
Step 3: Analyze the current expression
The expression I=a−2bt indicates that the current is a linear function of time t.
Step 4: Find the time when current reaches zero
To find when the current reaches zero, we set the expression for current equal to zero:
0=a−2bt
Solving for t:
2bt=a⟹t=a2b
Step 5: Determine the rate of change of current
Next, we find the rate of change of current by differentiating I:
dIdt=ddt(a−2bt)=−2b
Summary of Results
1. The expression for current is I=a−2bt.
2. The current reaches zero at t=a2b.
3. The rate of change of current is −2b.
Final Answer
Based on the analysis, we conclude:
- The current reaches a maximum and then decreases to zero at t=a2b.
- The rate of change of current is constant and equal to −2b.
2. The current reaches zero at t=a2b.
3. The rate of change of current is −2b.
- The current reaches a maximum and then decreases to zero at t=a2b.
- The rate of change of current is constant and equal to −2b.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:B. Assertion and reason
Explore 18 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Match the columns
Explore 4 Videos
- CURRENT ELECTRICITYBook:DC PANDEY ENGLISHChapter:CURRENT ELECTRICITYExercise:Check point
Explore 70 Videos
- COMMUNICATION SYSTEMBook:DC PANDEY ENGLISHChapter:COMMUNICATION SYSTEMExercise:Subjective
Explore 11 Videos
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEY ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:Medical entrances gallery
Explore 25 Videos
Similar Questions
The charge flowing in a conductor varies with time as Q=at−12bt2+16ct3 where a, b and c are positive constants. If at time t, the current in the conductor is i, which of the following graphs is correct ?
View SolutionThe current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View Solution
Knowledge Check
The charge flowing through a resistance R varies with time t as Q=at−bt2. The total heat produced in R is
Aa3RbBa3R2bCa3R3bDa3R6b
The current in conductor varies with time t as I=2t+3t2 where I is in ampere and t in seconds. Electric charge flowing through a section of the conductor during t=2sec to t=3sec is
View SolutionThe charge q flowing in a conductor of uniform cross section, varies with time as q=αt−bt2. Then, the current
View SolutionThe current in a conductor varies with time .t. as I=3t+4t2. Where I in amp and t in sec. The electric charge flows through the section of the conductor between t = 1s and t = 3s
View SolutionThe charge flowing throug a conductor beginning with time to=0 is given by the formula q=2t2+3t+1 (coulombs). Find the current i=dqdt at the end of the 5th seconds.
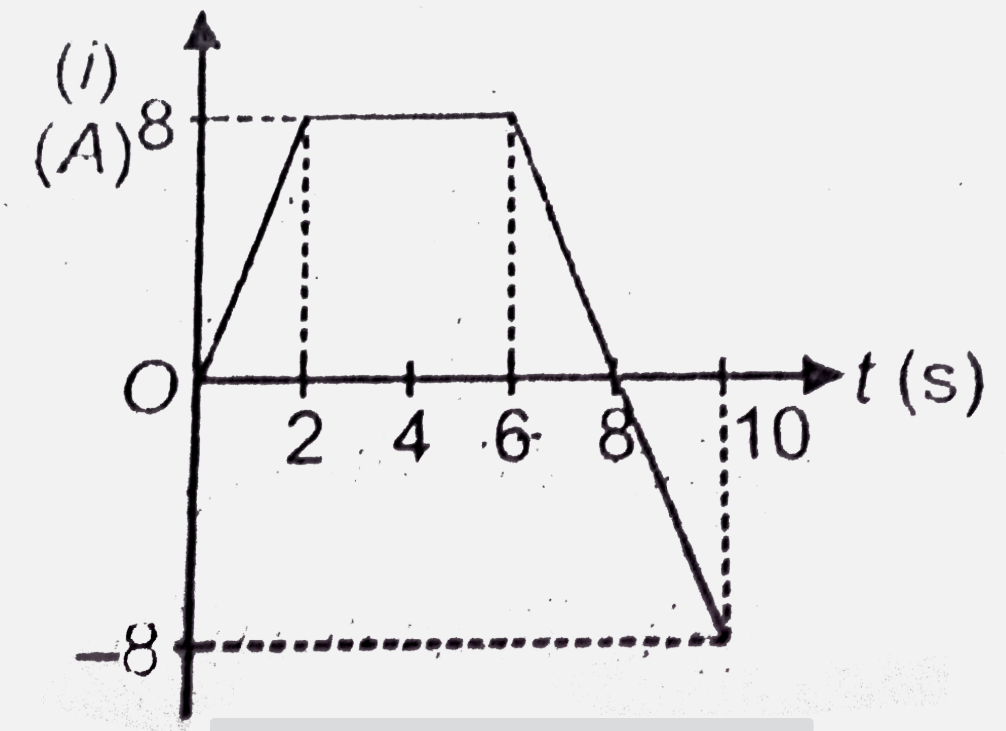
View SolutionThe current I through a conductor varies with time t as shown in figure. The average electric current during t=0 to t=10 s will be
View SolutionThe linear momentum of a particle varies with time t as p=a+bt+ct2. Then, whichh of the following is correct?
View SolutionIf charge through a cross-section of a conductor at timetis q=2t2+3t+1. Find the current at t = 2s.
View Solution