A 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
7200J
6200J
5200J
4200J
The correct Answer is:A
To solve the problem of how much heat energy is produced in a 50Ω resistor connected to a 10V battery over the course of one hour, we can follow these steps:
Step 1: Identify the given values
- Voltage (V) = 10 V
- Resistance (R) = 50 Ω
- Time (t) = 1 hour
Step 2: Convert time from hours to seconds
Since we need to calculate energy in Joules, we should convert the time into seconds:
t=1 hour=60 minutes×60 seconds/minute=3600 seconds
Step 3: Use the formula for heat energy produced
The heat energy (H) produced in a resistor can be calculated using the formula:
H=V2⋅tR
where:
- H is the heat energy in Joules,
- V is the voltage in volts,
- t is the time in seconds,
- R is the resistance in ohms.
Step 4: Substitute the values into the formula
Now, substituting the known values into the formula:
H=(10 V)2⋅(3600 s)50 Ω
Step 5: Calculate H
Calculating the square of the voltage:
(10 V)2=100 V2
Now substituting this back into the equation:
H=100⋅360050
Calculating the numerator:
100⋅3600=360000
Now divide by the resistance:
H=36000050=7200 J
Step 6: Conclusion
The heat energy produced in the resistor in one hour is:
H=7200 Joules
---
- Voltage (V) = 10 V
- Resistance (R) = 50 Ω
- Time (t) = 1 hour
Since we need to calculate energy in Joules, we should convert the time into seconds:
t=1 hour=60 minutes×60 seconds/minute=3600 seconds
The heat energy (H) produced in a resistor can be calculated using the formula:
H=V2⋅tR
where:
- H is the heat energy in Joules,
- V is the voltage in volts,
- t is the time in seconds,
- R is the resistance in ohms.
Now, substituting the known values into the formula:
H=(10 V)2⋅(3600 s)50 Ω
Calculating the square of the voltage:
(10 V)2=100 V2
Now substituting this back into the equation:
H=100⋅360050
Calculating the numerator:
100⋅3600=360000
Now divide by the resistance:
H=36000050=7200 J
The heat energy produced in the resistor in one hour is:
H=7200 Joules
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PRACTICE SHEET (EXERCISE - VI LEVEL-II (ADVANCED) (Straight Objective Type Questions))
Explore 3 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PRACTICE SHEET (EXERCISE - VI LEVEL-II (ADVANCED) (More than One correct Type Questions))
Explore 3 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PRACTICE SHEET (EXERCISE - V LEVEL-II (ADVANCED) (Integer Type Questions))
Explore 2 Videos
- CURRENT ELECTRICITYBook:AAKASH SERIESChapter:CURRENT ELECTRICITYExercise:PROBLEMS (LEVEL-II)
Explore 27 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:AAKASH SERIESChapter:DUAL NATURE OF RADIATION AND MATTERExercise:PRACTICE EXERCISEX
Explore 42 Videos
Similar Questions
A 10 V battery of negilgible internal resistance is connected across a 200V battery and a resistance of 38Ω as shown in figure.
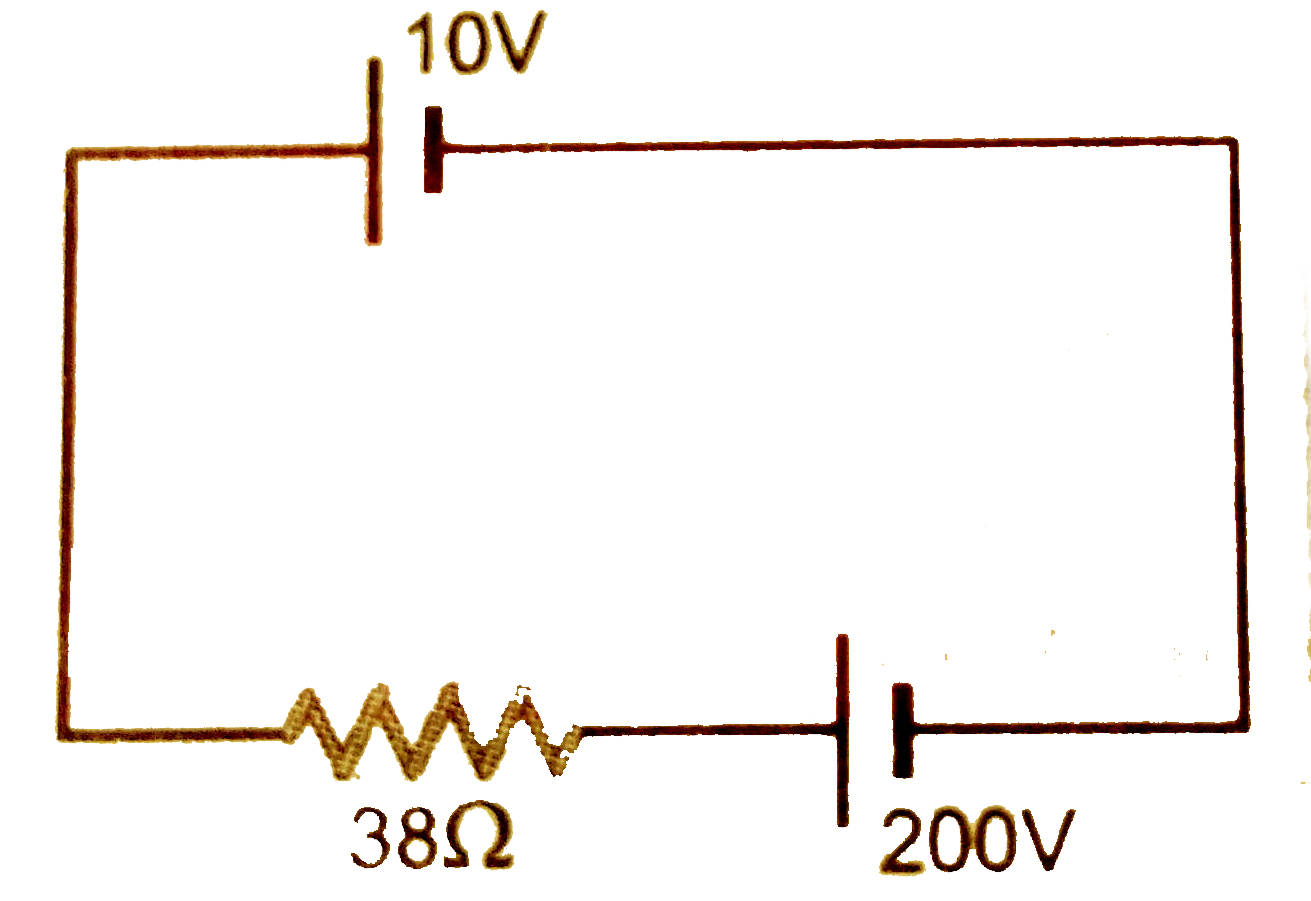 . Find the value of current in the circuit.
. Find the value of current in the circuit.
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View Solution
Knowledge Check
7 V battery with internal resistance 2Ωand3V battery with internal resistance 1Ω are connected to a 10Ω resistors as shown in figure, the current in 10Ω resistor is
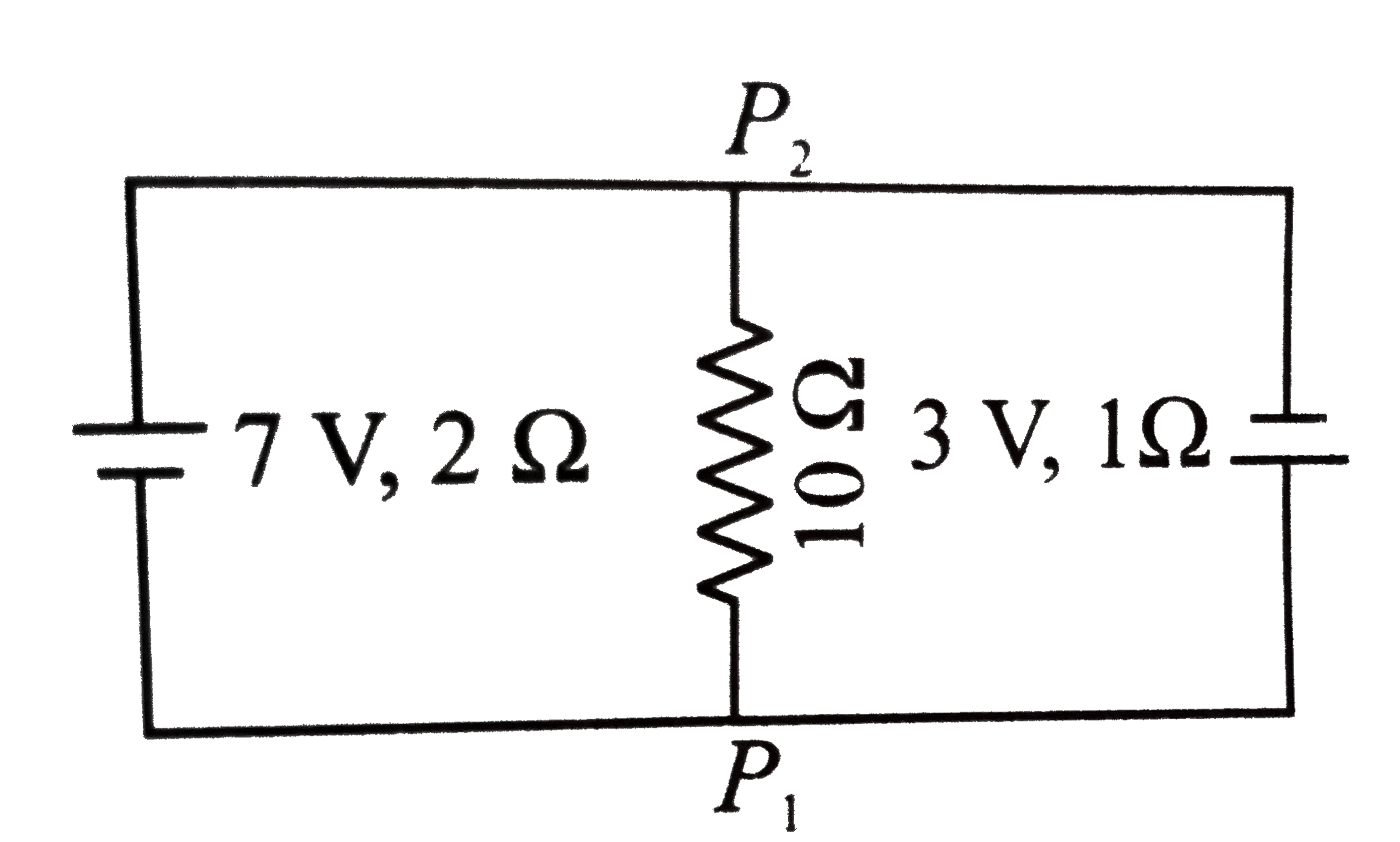 A0.27AB0.31AC0.031AD0.53
A0.27AB0.31AC0.031AD0.53
A 5 V battery of negligible internal resistance is connected across a 200 V battery and a resistance of 39Ω as shown in the figure. Find the value of the current.

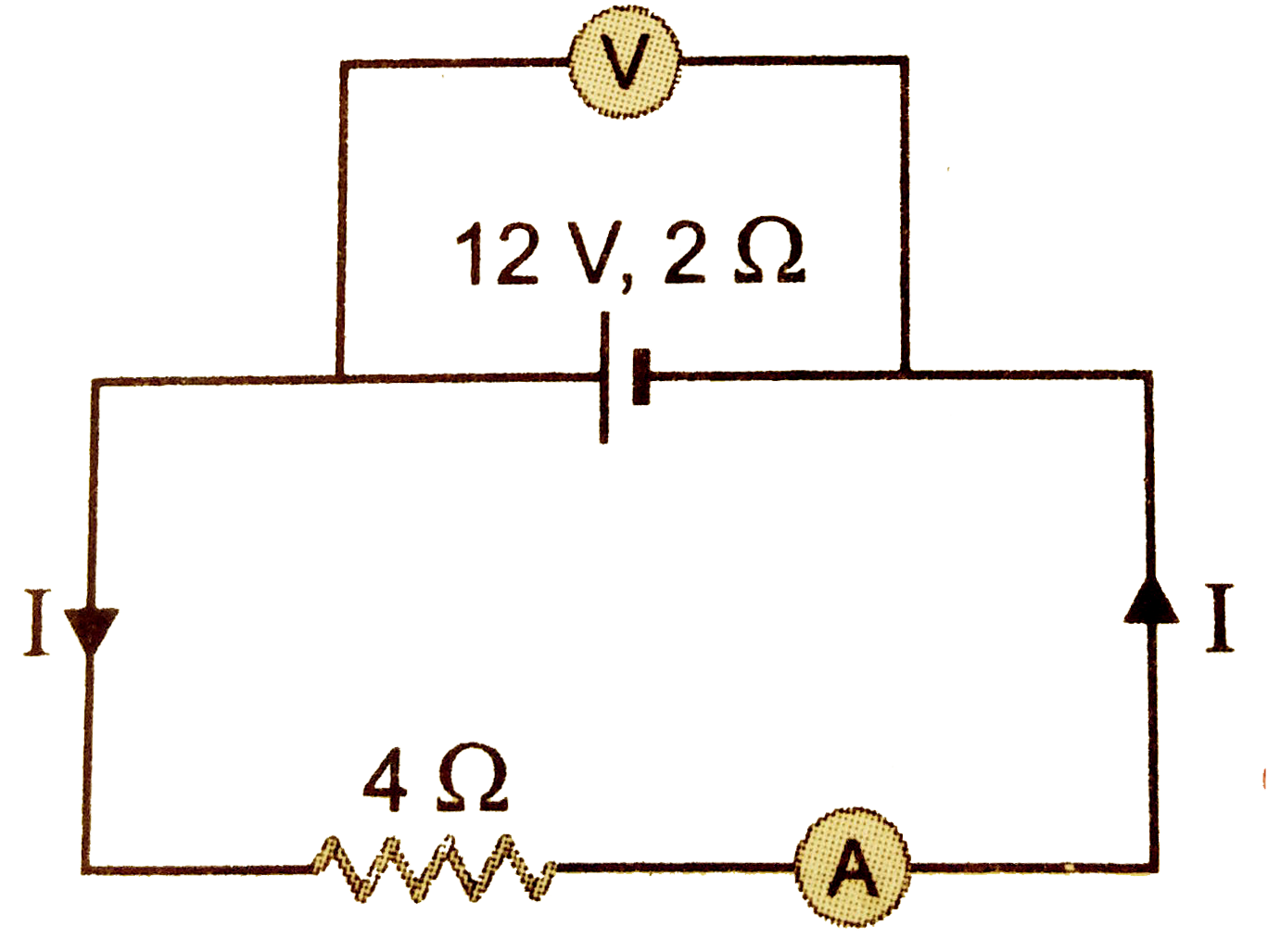
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
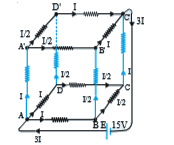
View SolutionA battery of 15 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 5Ω . Determine the equivalent resistance of the network and the current along each edge of the cube.
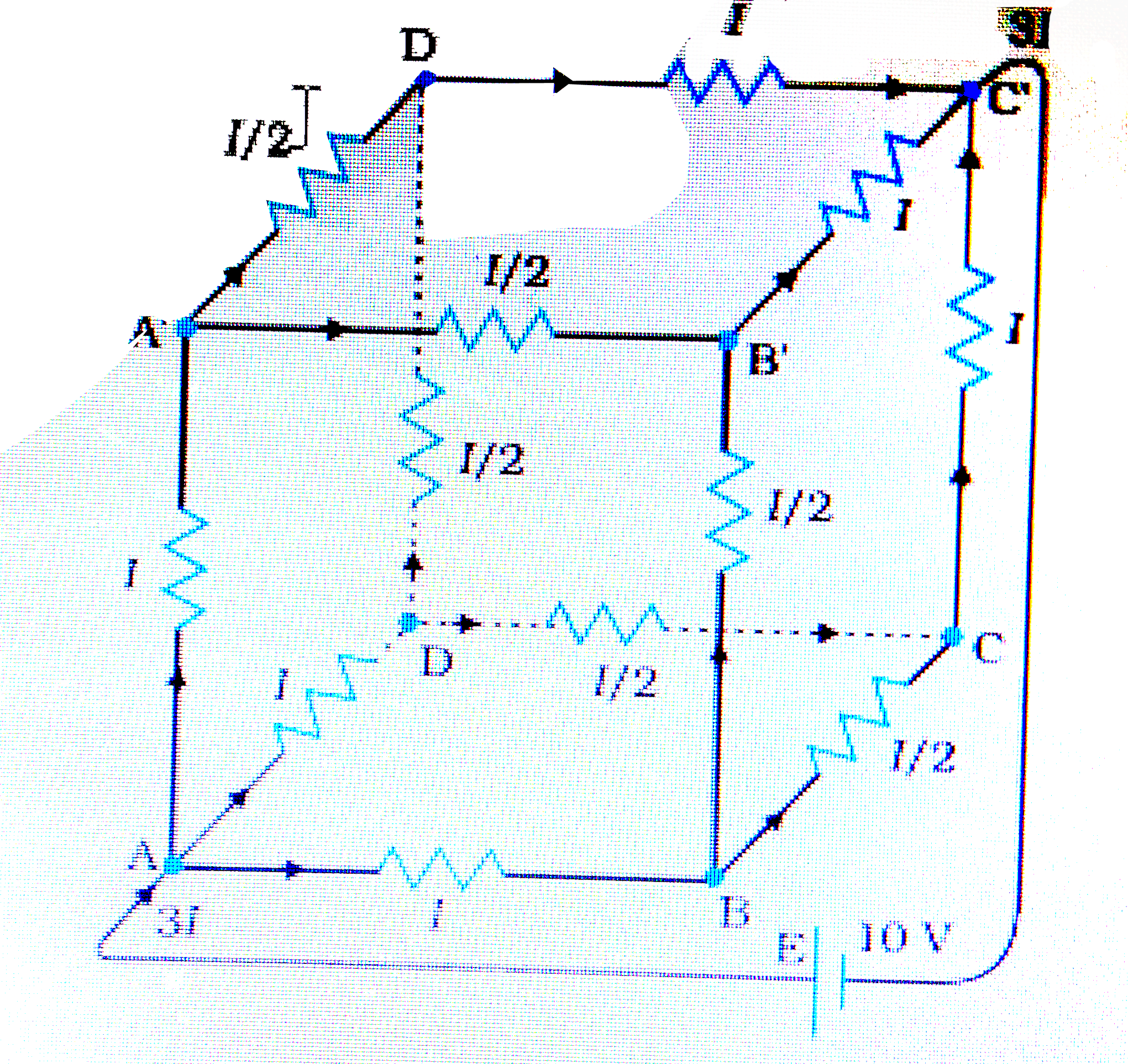
View SolutionBattery of 10 V and negligible internal resistance is connected across the diagonally opposite corners of a cubical network consisting of 12 resistors each of resistance 1Ω (Fig. 3.23). Determine the equivalent resistance of the network and the current along each edge of the cube.
View SolutionA 5V battery with internal resistance 2Ω and a 2V battery with internal resistance1Ω are connected to a 10Ω resistor as shown in the figure.

The current in the 10Ω resistor is
View SolutionA 5 V battery with internal resistance 1Ω and a 2 V battery with internal resistance 0.5Ω are connected to a 3Ω resistor as shown in the figure.The current in the 3Ω resistor is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View Solution

