Resistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
0.25 A
0.5 A
1.0 A
1.5 A
The correct Answer is:B
To solve the problem step by step, we need to analyze the circuit formed by the resistors and apply Ohm's law. Here’s how we can do it:
Step 1: Understand the Circuit Configuration
We have three resistors of 1 ohm, 2 ohm, and 3 ohm connected in a triangular configuration. The 1.5 V cell is connected across the 3 ohm resistor.
Step 2: Identify the Resistors
Let's label the resistors:
- R1 = 1 ohm
- R2 = 2 ohm
- R3 = 3 ohm
Step 3: Determine the Equivalent Resistance
Since the resistors are connected in a triangle, we can find the equivalent resistance between points A and C (across the 3 ohm resistor). The resistors R1 and R2 are in series with the 3 ohm resistor.
1. The equivalent resistance Req can be calculated using the formula for resistors in series:
Req=R1+R2=1ohm+2ohm=3ohm
2. Now, the total resistance in the circuit when the 3 ohm resistor is connected across the voltage source is:
Rtotal=Req∥R3=Req⋅R3Req+R3=3⋅33+3=96=1.5ohm
Step 4: Apply Ohm's Law to Find Current
Using Ohm's Law, we can find the current flowing through the 3 ohm resistor:
I=VR=1.5V1.5ohm=1A
Step 5: Determine Current Distribution
Since the current splits at the junction, we can find the current through the 3 ohm resistor. The voltage across the 3 ohm resistor is:
V=I⋅R3=1A⋅3ohm=3V
However, since we only have a 1.5 V source, the current through the 3 ohm resistor is:
I3ohm=1.5V3ohm=0.5A
Final Answer
The current flowing through the 3 ohm resistor is 0.5 A.
---
We have three resistors of 1 ohm, 2 ohm, and 3 ohm connected in a triangular configuration. The 1.5 V cell is connected across the 3 ohm resistor.
Let's label the resistors:
- R1 = 1 ohm
- R2 = 2 ohm
- R3 = 3 ohm
Since the resistors are connected in a triangle, we can find the equivalent resistance between points A and C (across the 3 ohm resistor). The resistors R1 and R2 are in series with the 3 ohm resistor.
Req=R1+R2=1ohm+2ohm=3ohm
Rtotal=Req∥R3=Req⋅R3Req+R3=3⋅33+3=96=1.5ohm
Using Ohm's Law, we can find the current flowing through the 3 ohm resistor:
I=VR=1.5V1.5ohm=1A
Since the current splits at the junction, we can find the current through the 3 ohm resistor. The voltage across the 3 ohm resistor is:
V=I⋅R3=1A⋅3ohm=3V
However, since we only have a 1.5 V source, the current through the 3 ohm resistor is:
I3ohm=1.5V3ohm=0.5A
The current flowing through the 3 ohm resistor is 0.5 A.
Similar Questions
If internal resistance of cell is negligible, then current flowing through the circuit is
View SolutionA 10 V storage battery of negligible internal resistance is connected across a 50Ω resistor. How much heat energy is produced in the resistor in 1 hour
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
View SolutionWhen connected across the terminals of a cell, a voltmeter measures 5 V and a connected ammeter measures 10 A of current. A resistance of 2 ohm s is connected across the terminals of the cell. The current flowing through this resistance will be
View SolutionA uniform wire of resistance 9Ω is cut into 3 equal parts. They are connected in form of equilateral triangle ABC. A cell of e.m.f. 2V and negligible internal resistance is connected across B and C. Potential difference across AB is
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionA 50V battery is connected across a 10 ohm resistor. The current is 4.5A is flowing through the resistor then the internal resistance of the battery is
View SolutionTwo resistances of 100 ohm and 200 ohm are connected in series with a battery of emf 4 volt and negligible internal resistance. A voltmeter of resistance 200 ohm is used to measure voltage across the two resistances separately. Calculate the voltage indicated.
View SolutionTwo resistors of 2.0 92 and 3.0 22 are connected
in parallel, with a battery of 60 V and negligible internal resistance. For each case draw a circuit diagram and calculate the current through the battery
View SolutionThree equal resistace, each of R ohm, are connectedd as shown in the figure. A battery of 2V and of internal resistance 0.1 ohm is connected across the circuit. The value of R for which the heat generated in the circuit maximum will be
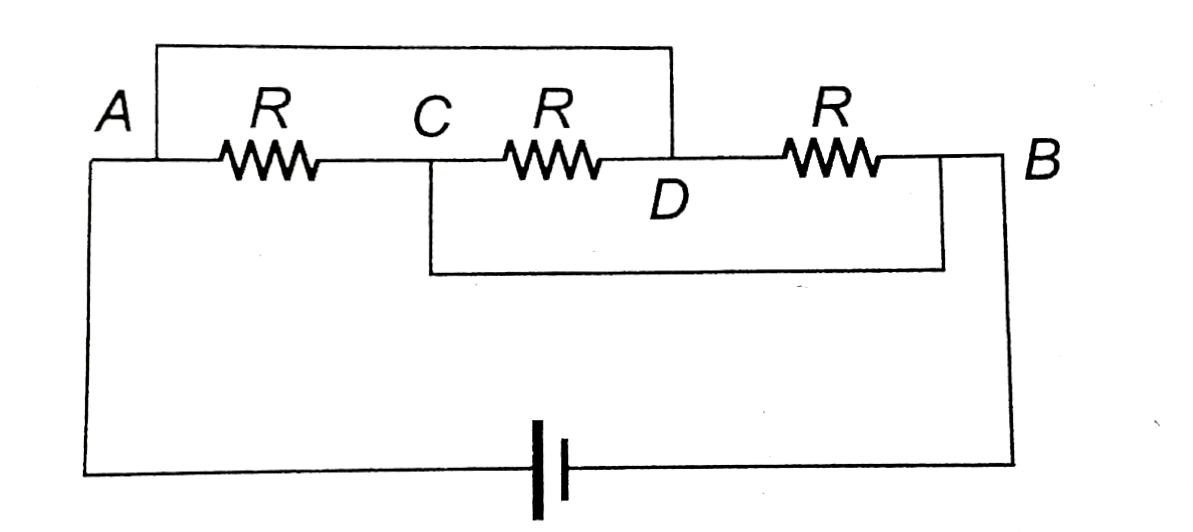
View Solution
