Two wires wrapped over a conical form the loops 1 and 2. If they produce no net magnetic field at the apex P, find the value of i1i2
Magnetic induction due to a loop at apex,
B=μ0ir22(r2+x2)3/2
But r2+x2=l2⇒(r2+x2)3/2=l3 where .l. is slant length B=μ0i2r(rl)3
But rl=sinϕ where ϕ is apex angle, same for both the loops →B1+→B2=0 (given) ⇒B1=B2⇒i1i2=r1r2
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
Two wires are wrapped over a wooden cylinder to form two coaxial loops carrying currents i1 and i2. If i2=8i1 then find tlte value of x for B = 0 at the origin O
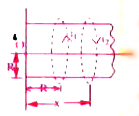View SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
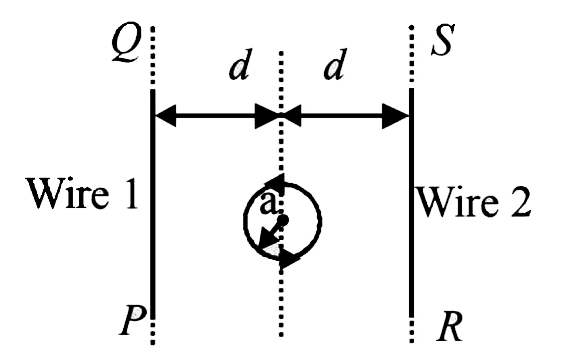
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that caseView Solution
Knowledge Check
- Question 1 - Select One
A steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
A1B5C10D7
The figure shows a circular loop of radius a with two long parallel wires (numbered 1 and 2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop . In that caseView SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.
View SolutionTwo concentric coplanar circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to i1 alone at the centre. if r2=2r1. the value of i2/i1 is
View SolutionThe dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B1 . When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B2 . The ratio B1B2 is:
View SolutionThe entire network shown here, has uniform wire having resistance per unit length as 1Ω/m. It is placed in a uniform but time varying magnetic field →B(directed into the plane). If the strength of the magnetic field is increasing at 1T/s, the ratio I1/I2 equals
View SolutionCalculate the magnitude of the magnetic field at point P as shown in Fig, in terms of R,I1andI2.
View SolutionIn the diagram shown, I1,I2 are the magnitudes of current in the squre loop and infinite long straight conductor respectively. If the net magnetic field at the centre of the loop is zero, then the relation between I1andI2 is
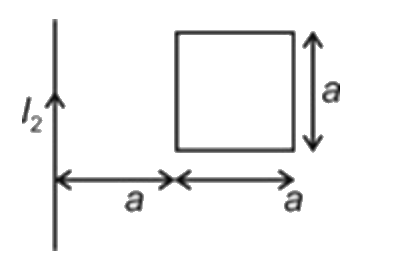View Solution