Two concentric coplanar circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to i1 alone at the centre. if r2=2r1. the value of i2/i1 is
2
1/2
1/4
1
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Understand the Magnetic Field Due to Each Loop
The magnetic field at the center of a circular loop carrying current i is given by the formula:
B=μ0i2r
where μ0 is the permeability of free space, i is the current, and r is the radius of the loop.
Step 2: Calculate the Magnetic Field for Each Loop
For the first loop with radius r1 and current i1:
B1=μ0i12r1
For the second loop with radius r2 and current i2:
B2=μ0i22r2
Step 3: Substitute the Given Relationship Between the Radii
We are given that r2=2r1. Thus, we can substitute r2 in the equation for B2:
B2=μ0i22(2r1)=μ0i24r1
Step 4: Determine the Net Magnetic Field at the Center
The net magnetic field at the center of the loops, considering that the currents are in opposite directions, is given by:
Bnet=B1−B2
Substituting the expressions for B1 and B2:
Bnet=μ0i12r1−μ0i24r1
Step 5: Simplify the Expression for the Net Magnetic Field
Factoring out μ0r1:
Bnet=μ0r1(i12−i24)
Step 6: Set Up the Given Condition
According to the problem, the net magnetic field is half of the magnetic field due to i1 alone:
Bnet=12B1=12(μ0i12r1)=μ0i14r1
Step 7: Equate the Two Expressions for the Net Magnetic Field
Setting the two expressions for Bnet equal to each other:
μ0r1(i12−i24)=μ0i14r1
Step 8: Cancel Out Common Terms
Since μ0 and r1 are common on both sides, we can simplify:
i12−i24=i14
Step 9: Solve for i2
Rearranging gives:
i12−i14=i24
2i14−i14=i24
i14=i24
Thus, we find:
i2=i1
Step 10: Calculate the Ratio i2i1
Finally, we compute the ratio:
i2i1=1
Final Answer
The value of i2i1 is 1.
---
The magnetic field at the center of a circular loop carrying current i is given by the formula:
B=μ0i2r
where μ0 is the permeability of free space, i is the current, and r is the radius of the loop.
For the first loop with radius r1 and current i1:
B1=μ0i12r1
B2=μ0i22r2
We are given that r2=2r1. Thus, we can substitute r2 in the equation for B2:
B2=μ0i22(2r1)=μ0i24r1
The net magnetic field at the center of the loops, considering that the currents are in opposite directions, is given by:
Bnet=B1−B2
Substituting the expressions for B1 and B2:
Bnet=μ0i12r1−μ0i24r1
Factoring out μ0r1:
Bnet=μ0r1(i12−i24)
According to the problem, the net magnetic field is half of the magnetic field due to i1 alone:
Bnet=12B1=12(μ0i12r1)=μ0i14r1
Setting the two expressions for Bnet equal to each other:
μ0r1(i12−i24)=μ0i14r1
Since μ0 and r1 are common on both sides, we can simplify:
i12−i24=i14
Rearranging gives:
i12−i14=i24
2i14−i14=i24
i14=i24
Thus, we find:
i2=i1
Finally, we compute the ratio:
i2i1=1
The value of i2i1 is 1.
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Subjective type
10 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type
14 Videos
Similar Questions
Two coplanar circular coils of equal radius carrying currents i1,i2 in opposite directions are at a large distance 'd'. The distance from the first coil where the resultant magnetic induction is zero is
View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionTwo coplanar concentric circular coils of radii r and 2r, have the same number of turns n. The smaller coil carries a clockwise current i, while the larger coil carries an anticlockwise current 2i. The magnetic field induction at the centre is
View SolutionIn the figure shown there are two semicircles of radii r1 and r2 in which a current i is flowing. The magnetic induction at the centre O will be

View SolutionIn the figure shown there are two semicircles of radii r1 and r2 in which a current i is flowing. The magnetic induction at the centre O will be

View SolutionCircular loop of a wire and a long straight wire carry current Ic and Ierespectively as shown in figure. Assuming that these are placed in the same plane. The magnetic field will be zero at the centre of the loop when the separation H is:
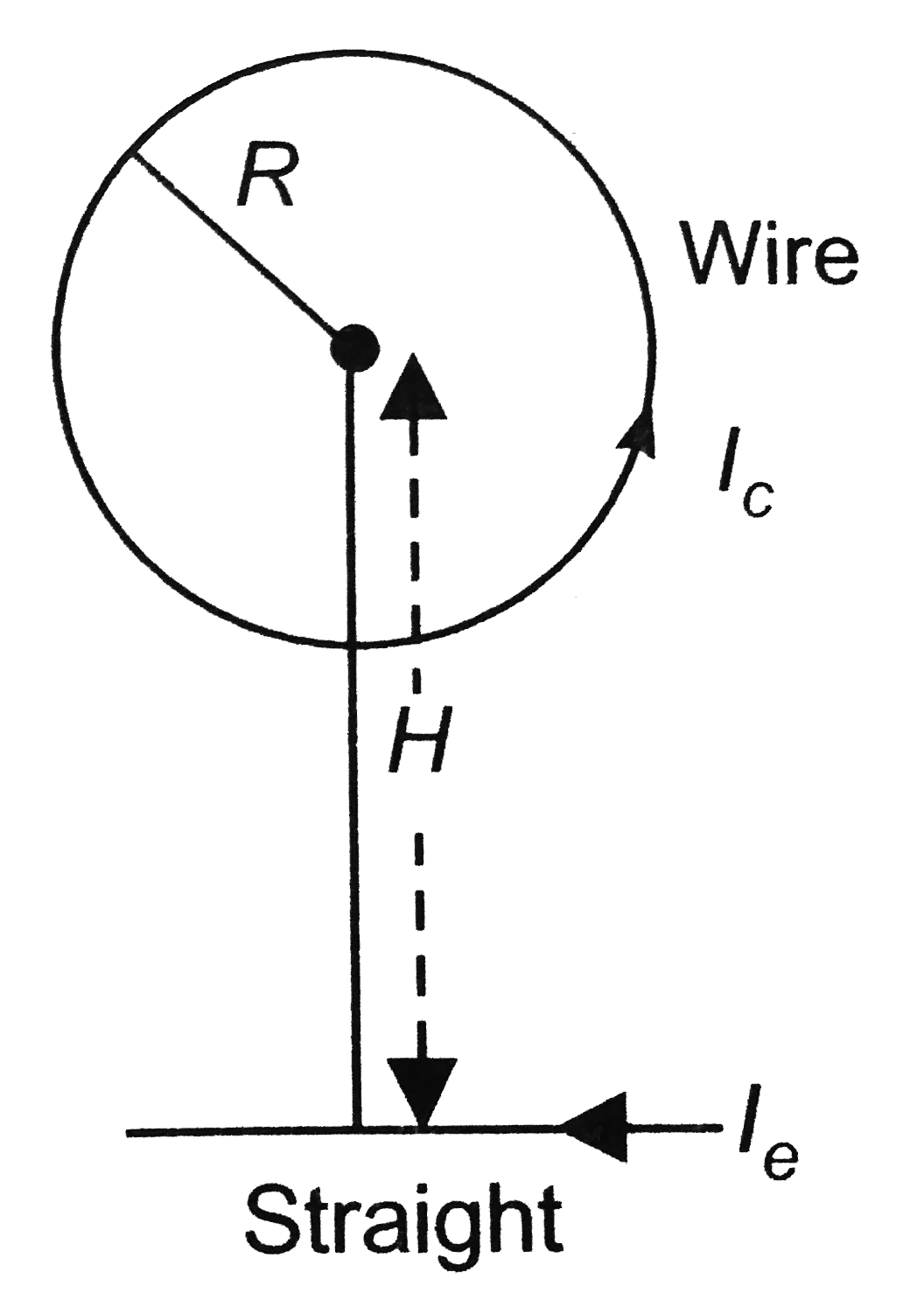
View SolutionTwo concentric circular coils of radii R and r (<<R) carry currents of i1 and i2 respectively. If the smaller coil is rotated slightly about one of its diameter, it starts oscillating. Then, which of the following statement(s) is/are correct ?

View SolutionA circular loop of radius r carries a current i. where should a long , straight wire carrying a current 4i be placed in the plane of the circle so that the magnetic field at the centre becomes zero?
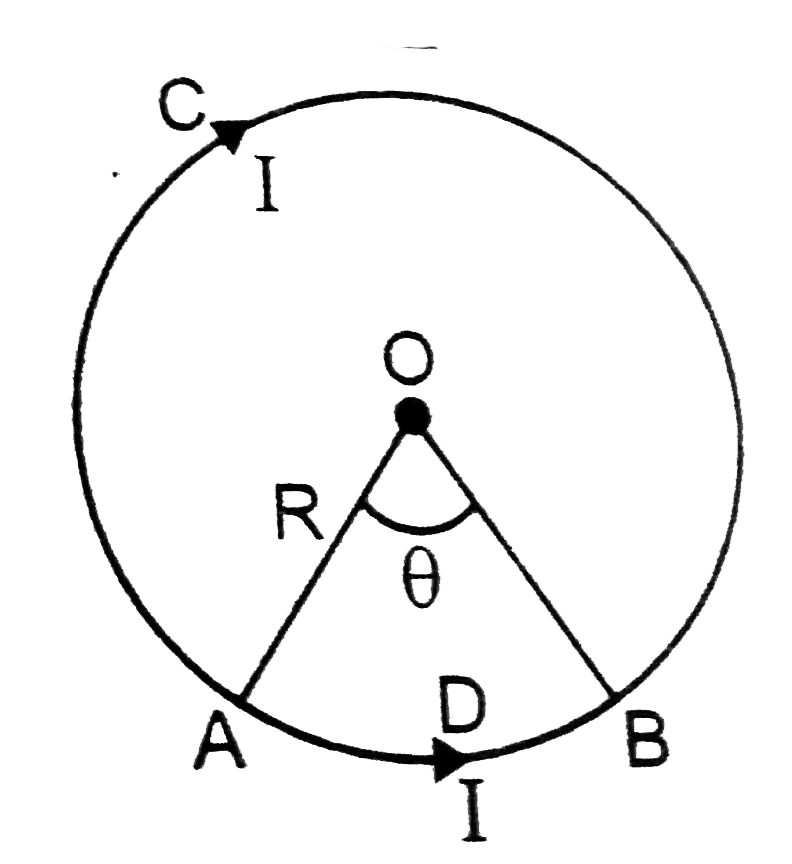
View SolutionEqual current I flows in two segments of a circular loop in the direction shown in figure. Radius of loop is R. What is the magnitude of magnetic field induciton at the centre of the loop?
View SolutionTwo similar circular loops of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are I and I√3 respectively. The magnetic field at the centre of the coil is
View Solution
