A long straight current carrying conductor has a current from -z to +z, then find the magnetic induction at a point P(x, y, 0) in vectorial notation (ˆi,ˆj,ˆk) are unit vector along x,y, z axis)

B=μ02πIr
=μ02πI√x2+y2[−sinθˆi+cosθˆj]
=μ02πI√x2+y2[−y√x2+y2i+x√x2+y2j]
=μ02πI(x2+y2)(−yˆi+xˆj)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA142videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
The figure shows a long straight current carrying conductor. Can you plot the variation of magnetic field on x-axis ?
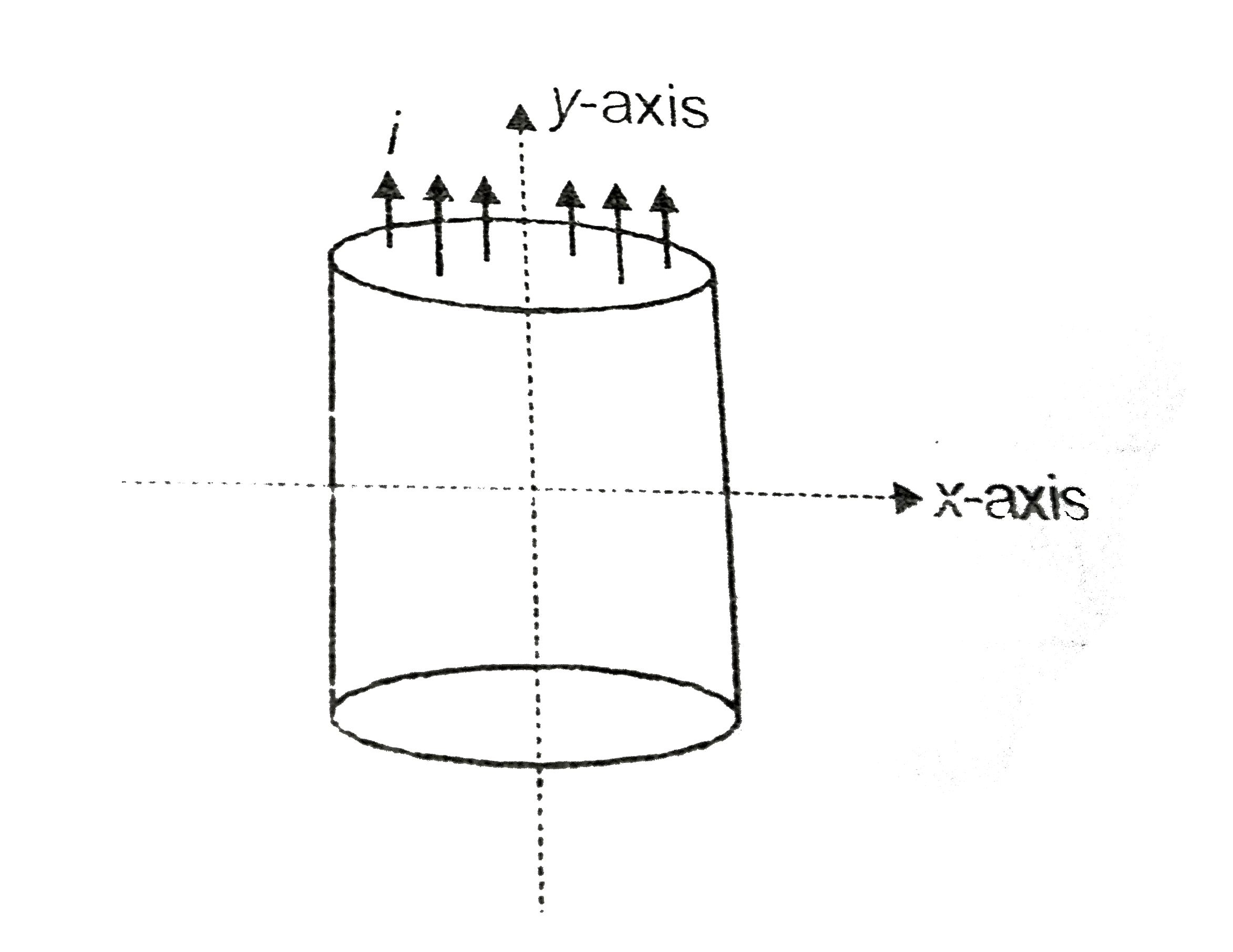 View Solution
View SolutionThe angle θ between the vector p=ˆi+ˆj+ˆk and unit vector along X-axis is
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionTwo long straight currents carrying wires having currents I and 2I lie along y-and z-axis, respectively, as shown in Fig. Find →B at a point P(x,0).
 View Solution
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionFind the distance between the planes 2x - 3y + 6z+8= 0 and →r.(2ˆi−3ˆj+6ˆk)=−4
View SolutionAn infinite current-carrying conductor is placed along the z-axis and a wire loop is kept in the x−y plane. The current in the conductor is increasing with time. Then the
View SolutionTwo long straight conductors with current I1 and I2 are placed along X and Y axes. The equation of locus of points of zero magnetic induction is :
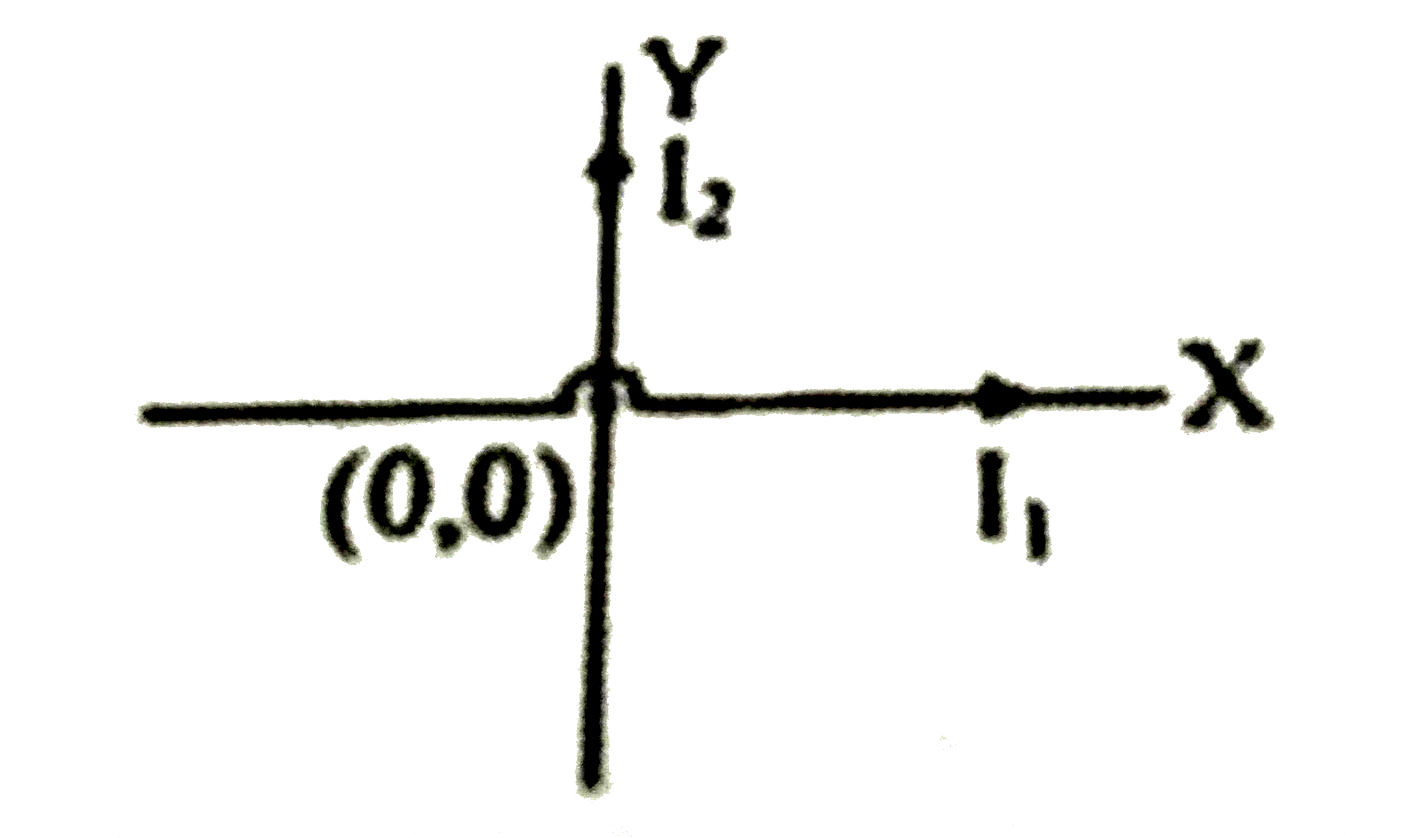 View Solution
View SolutionWhat vector must be added to the two vectors 2ˆi−ˆj+3ˆk and 3ˆi−2ˆj−2ˆk, so that the resultant may be a unit vector along z- axis
View Solution

