A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
Increases the speed of the particle
Decreases the kinetic energy of the particle.
Changes the direction of motion of the particle
Both 1 and 3
The correct Answer is:C
To solve the problem of a charged particle entering a uniform magnetic field perpendicular to its motion, we can follow these steps:
1. Understanding the Scenario:
- A charged particle (let's say with charge Q) is moving with a velocity →V and enters a uniform magnetic field →B that is perpendicular to the velocity of the particle.
2. Applying the Lorentz Force:
- The force acting on the charged particle due to the magnetic field is given by the Lorentz force equation:
→F=Q(→V×→B)
- Since the magnetic field is perpendicular to the velocity, the angle between →V and →B is 90∘.
3. Direction of the Force:
- The direction of the force →F can be determined using the right-hand rule. If you point your fingers in the direction of →V and curl them towards →B, your thumb will point in the direction of the force →F.
4. Effect on the Motion of the Particle:
- The force →F is always perpendicular to the velocity →V. This means that while the speed of the particle remains constant, the direction of the velocity changes.
- As a result, the particle will move in a circular path due to the centripetal nature of the force acting on it.
5. Work Done and Kinetic Energy:
- Since the force is perpendicular to the displacement of the particle, the work done by the magnetic force is zero:
W=→F⋅→d=0
- Because the work done is zero, there is no change in the kinetic energy of the particle. The speed of the particle remains constant.
6. Conclusion:
- The correct answer to the question is that the magnetic field changes the direction of motion of the particle, but it does not change its speed or kinetic energy. Therefore, the correct option is:
- Option 3: Changes the direction of motion of the particle.
- A charged particle (let's say with charge Q) is moving with a velocity →V and enters a uniform magnetic field →B that is perpendicular to the velocity of the particle.
- The force acting on the charged particle due to the magnetic field is given by the Lorentz force equation:
→F=Q(→V×→B)
- Since the magnetic field is perpendicular to the velocity, the angle between →V and →B is 90∘.
- The direction of the force →F can be determined using the right-hand rule. If you point your fingers in the direction of →V and curl them towards →B, your thumb will point in the direction of the force →F.
- The force →F is always perpendicular to the velocity →V. This means that while the speed of the particle remains constant, the direction of the velocity changes.
- As a result, the particle will move in a circular path due to the centripetal nature of the force acting on it.
- Since the force is perpendicular to the displacement of the particle, the work done by the magnetic force is zero:
W=→F⋅→d=0
- Because the work done is zero, there is no change in the kinetic energy of the particle. The speed of the particle remains constant.
- The correct answer to the question is that the magnetic field changes the direction of motion of the particle, but it does not change its speed or kinetic energy. Therefore, the correct option is:
- Option 3: Changes the direction of motion of the particle.
Topper's Solved these Questions
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION C
47 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - ASSIGNMENT (SECTION A)
34 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - J)
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
Similar Questions
A charged particle enters in a uniform magnetic field perpendicular to it. Now match the following two columns.

View SolutionThe path of a charged particle in a uniform magnetic field, when the velocity and the magnetic field are perpendicular to each other is a
View SolutionStatement 1: If a proton and an α-particle enter a uniform magnetic field perpendicularly with the same speed, the time period of revolution of α-particle is double than that of proton.
Statement 2: In a magnetic field, the period of revolution of a charged particle is directly proportional to the mass of the particle and inversely proprotional to the charge of particle.
View SolutionStatement 1: If a proton and an α-particle enter a uniform magnetic field perpendicularly with the same speed, the time period of revolution of α-particle is double than that of proton.
Statement 2: In a magnetic field, the period of revolution of a charged particle is directly proportional to the mass of the particle and inversely proprotional to the charge of particle.
View SolutionWhen a charged particle enters a uniform magnetic field its kinetic energy
View SolutionA charged particle moves through a magnetic field perpendicular to its direction. Then
View SolutionA charge particle of charge 'q' and mass 'm' enters in a given magnetic field 'B' and perpendicular to the magnetic field as shown in the figure. It enters at an angle of 60∘ with the boundary surface of magnetic field and comes out at an angle of 30∘ with the boundary surface of the magnetic field as shown in the figure. Find width 'd' in which magnetic field exist.
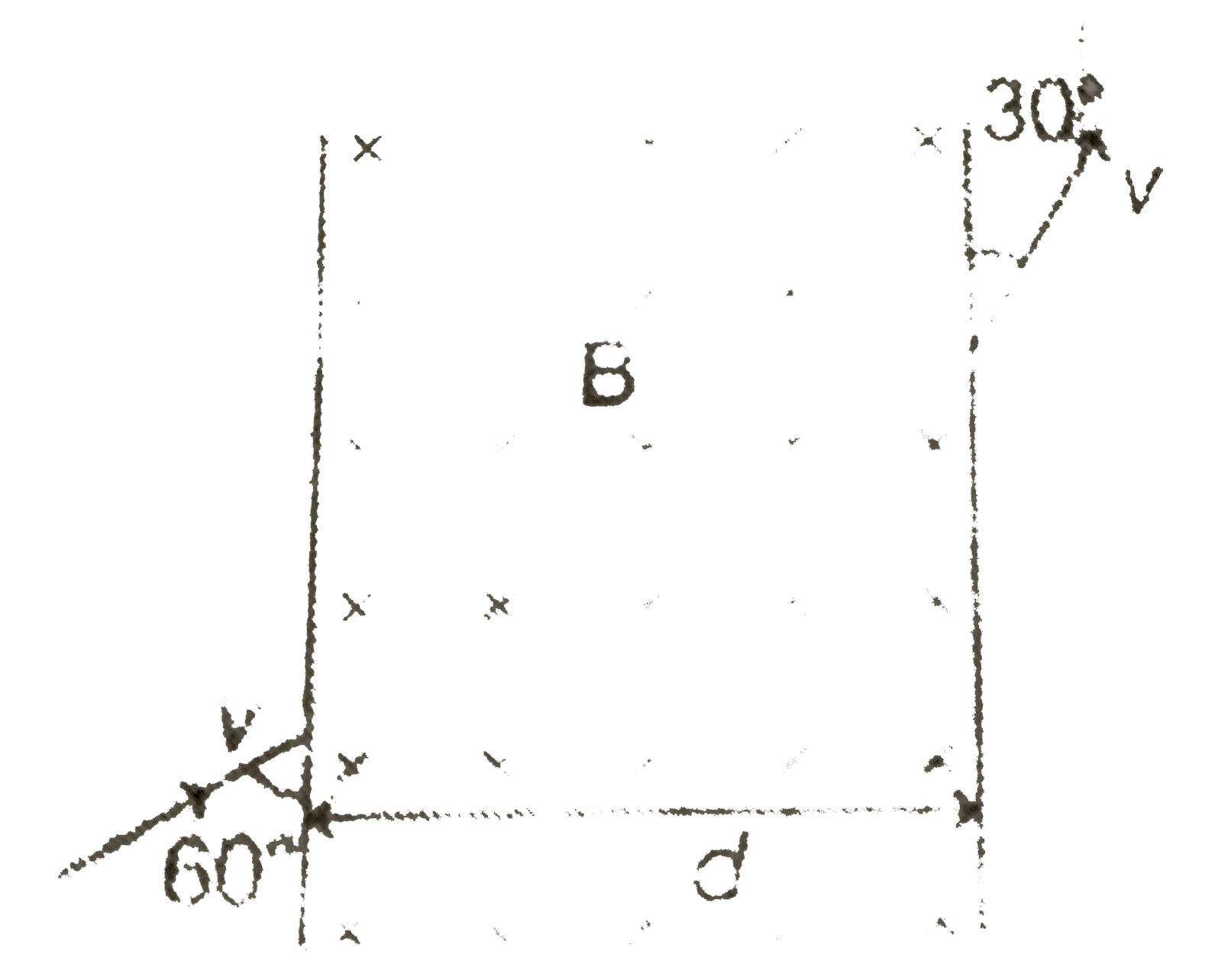
View SolutionA neutron, a proton, an electron and an α−particle enter a region of uniform magnetic field with equal velocities. The magnetic field is perpendicular to the paper and directed into it. The tracks of particles are labeled in Fig. 1.132. The neutron follows the track

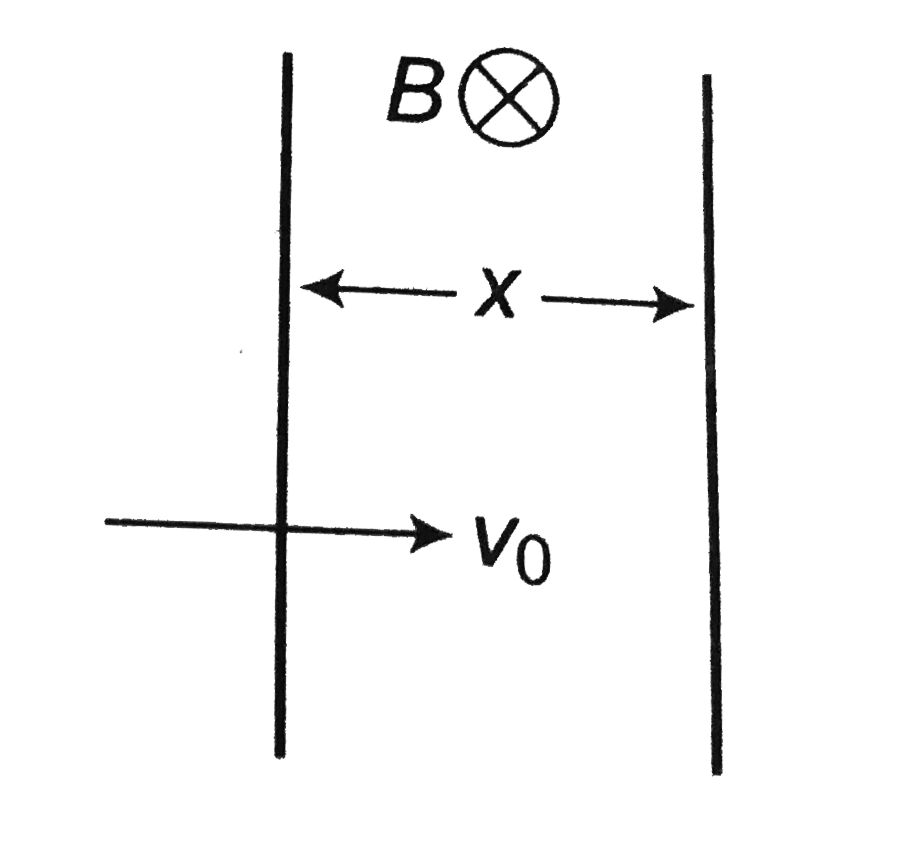
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
View SolutionA charged particle enters a unifrom magnetic field with velocity vector at an angle of 45∘ with the magnetic field . The pitch of the helical path followed by the particles is ρ . The radius of the helix will be
View Solution
