A circular arc of wire subtends an angle /2 at the centre. If it carries a current i and its radius of curvature is R then the magnetic field at the centre of the arc is
The correct Answer is:D
To solve the problem of finding the magnetic field at the center of a circular arc of wire that subtends an angle of π2 at the center, we can follow these steps:
1. Identify the Formula:
The magnetic field B at the center of a circular arc carrying current i and subtending an angle θ is given by the formula:
B=μ0i4πr⋅θ
where:
- B is the magnetic field,
- μ0 is the permeability of free space,
- i is the current,
- r is the radius of the arc,
- θ is the angle in radians.
2. Substitute the Given Values:
In this case, we have:
- θ=π2,
- r=R (the radius of curvature).
Plugging these values into the formula:
B=μ0i4πR⋅π2
3. Simplify the Expression:
Now, simplify the expression:
B=μ0i⋅π4πR⋅2
This simplifies to:
B=μ0i8R
4. Final Result:
Thus, the magnetic field at the center of the arc is:
B=μ0i8R
Conclusion:
The magnetic field at the center of the circular arc is given by:
B=μ0i8R
The magnetic field B at the center of a circular arc carrying current i and subtending an angle θ is given by the formula:
B=μ0i4πr⋅θ
where:
- B is the magnetic field,
- μ0 is the permeability of free space,
- i is the current,
- r is the radius of the arc,
- θ is the angle in radians.
In this case, we have:
- θ=π2,
- r=R (the radius of curvature).
B=μ0i4πR⋅π2
Now, simplify the expression:
B=μ0i⋅π4πR⋅2
This simplifies to:
B=μ0i8R
Thus, the magnetic field at the center of the arc is:
B=μ0i8R
The magnetic field at the center of the circular arc is given by:
B=μ0i8R
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
The magnetic field at centre O of the arc in Fig.
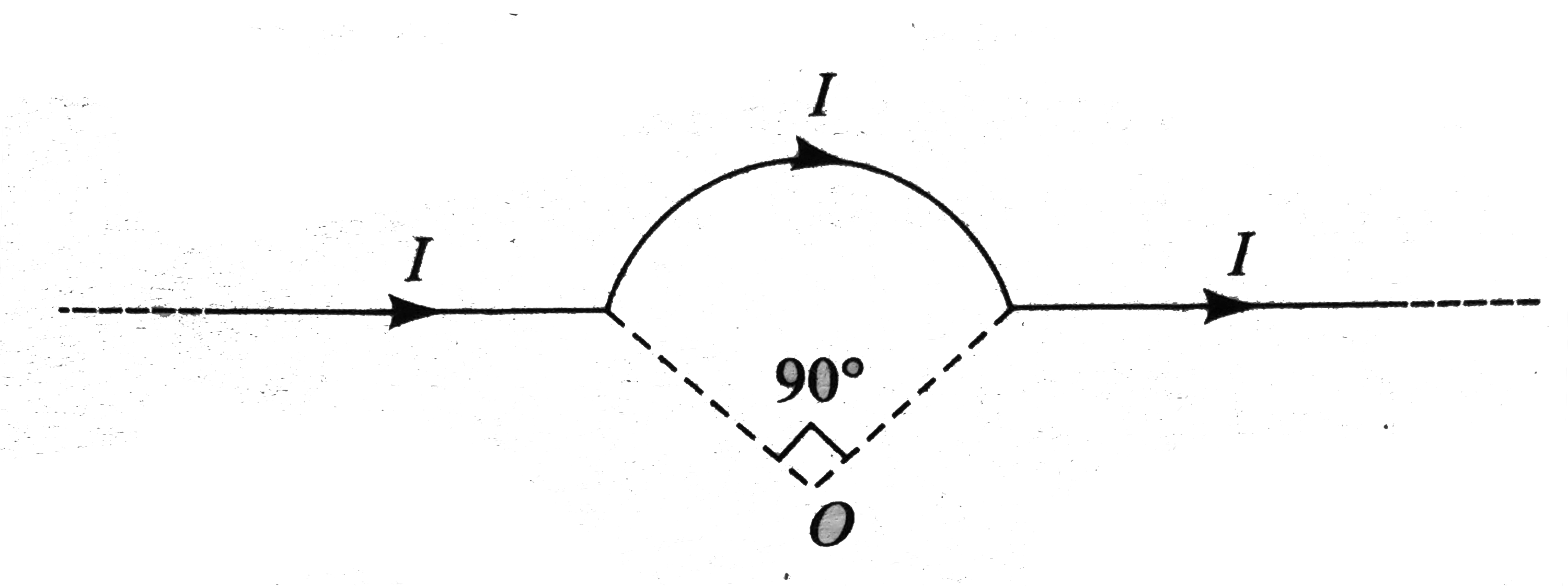 View Solution
View SolutionAn arc of a circle of raduis R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionAn arc of length 20π cm subtends an angle of 144o at the centre of a circle. Find the radius of the circle.
View Solution
A conducting wire carrying a current I is bent into the shape as shown. The net magnetic field at the centre O of the circular arc of radius RView SolutionA long wire bent as shown in fig. carries current I. If the radius of the semicircular portion is a, the magnetic field at centre C is
 View Solution
View SolutionA circular arc of length π cm. Find angle subtended by it at the centre in radian and degree.
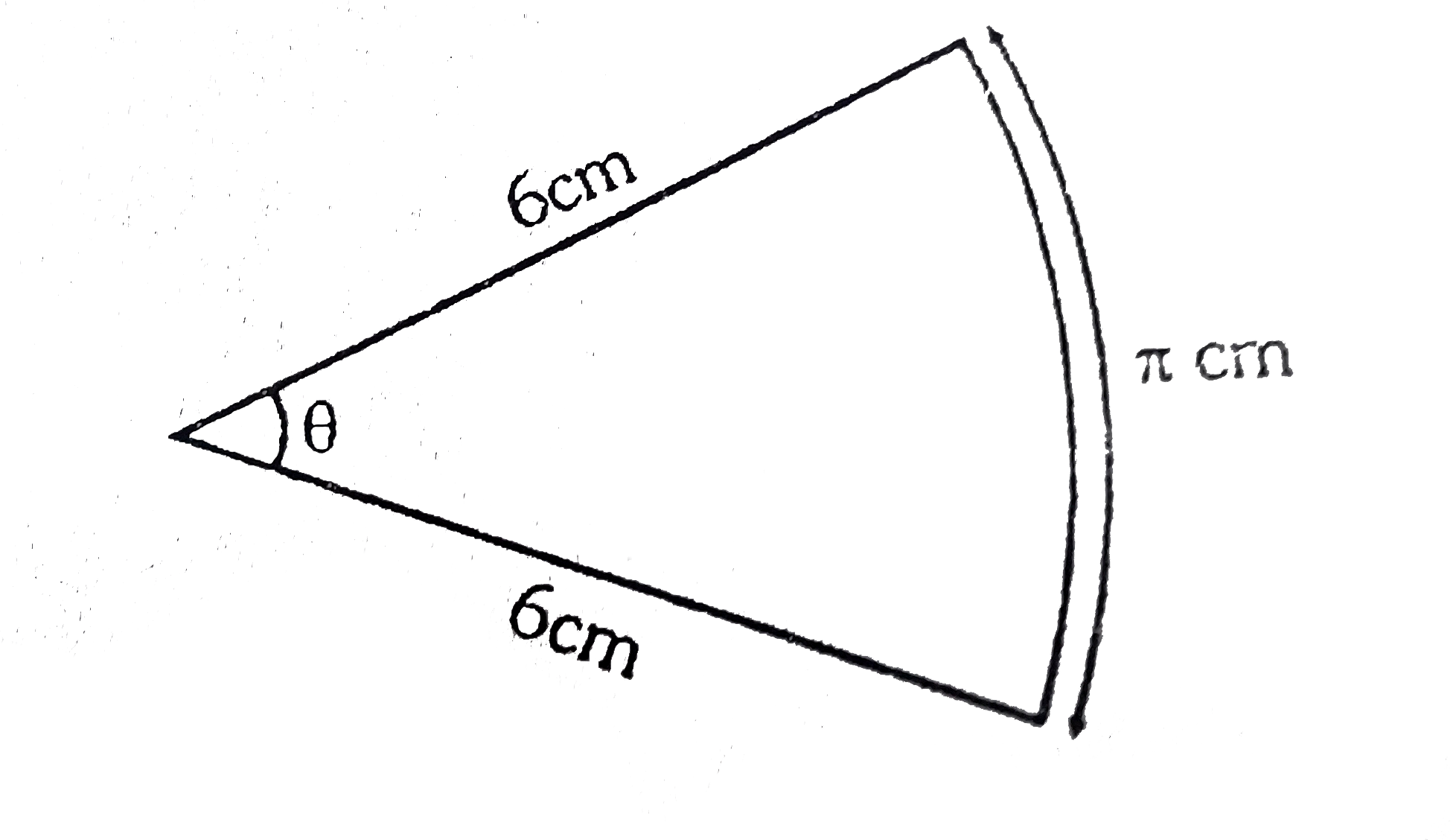 View Solution
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is :
 View Solution
View SolutionA part of a long wire carrying a current i is bent into a circle of radius r as shown in figure. The net magnetic field at the centre O of the circular loop is
 View Solution
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View Solution

