An arc of a circle of raduis R subtends an angle π2 at the centre. It carriers a current i. The magnetic field at the centre will be
μ0i2R
μ0i8R
(mu_(0)i)/(4R)
2μ0i5R
The correct Answer is:B
To find the magnetic field at the center of an arc of a circle that subtends an angle of π2 at the center and carries a current i, we can follow these steps:
Step 1: Understand the formula for the magnetic field due to a circular arc
The magnetic field B at the center of a circular arc carrying a current can be derived from the Biot-Savart Law. For a full circular loop, the magnetic field at the center is given by:
B=μ0I2R
where μ0 is the permeability of free space, I is the current, and R is the radius of the circular arc.
Step 2: Adjust the formula for the angle subtended by the arc
Since the arc subtends an angle θ at the center, we need to adjust the formula to account for the fraction of the full circle represented by this angle. The total angle of a full circle is 2π. Therefore, the magnetic field due to the arc can be expressed as:
B=μ0I2R⋅θ2π
Step 3: Substitute the given angle into the formula
In this case, the angle θ is given as π2. Substituting this value into the formula gives:
B=μ0I2R⋅π22π
Step 4: Simplify the expression
Now, we simplify the expression:
B=μ0I2R⋅14=μ0I8R
Conclusion
Thus, the magnetic field at the center of the arc is:
B=μ0I8R
Final Answer
The magnetic field at the center of the arc is μ0I8R.
---
The magnetic field B at the center of a circular arc carrying a current can be derived from the Biot-Savart Law. For a full circular loop, the magnetic field at the center is given by:
B=μ0I2R
where μ0 is the permeability of free space, I is the current, and R is the radius of the circular arc.
Since the arc subtends an angle θ at the center, we need to adjust the formula to account for the fraction of the full circle represented by this angle. The total angle of a full circle is 2π. Therefore, the magnetic field due to the arc can be expressed as:
B=μ0I2R⋅θ2π
In this case, the angle θ is given as π2. Substituting this value into the formula gives:
B=μ0I2R⋅π22π
Now, we simplify the expression:
B=μ0I2R⋅14=μ0I8R
Thus, the magnetic field at the center of the arc is:
B=μ0I8R
The magnetic field at the center of the arc is μ0I8R.
Topper's Solved these Questions
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Taking it together
75 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Assertion and reason
20 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Level 2 Subjective
5 Videos
- MAGNETICSBOOK - DC PANDEY ENGLISHCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
Similar Questions
A square loop of side a carris a current I. The magnetic field at the centre of the loop is
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionA current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

View SolutionA current i ampere flows in a circular arc of wire whose radius is R, which subtend an angle 3π/2 radian at its centre. The magnetic induction B at the centre is

View SolutionA wire bent in the form of a sector of radius r subtending an angle θ∘ at centre as shown in figure is carrying a current I. The magnetic field at O is :
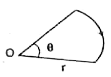
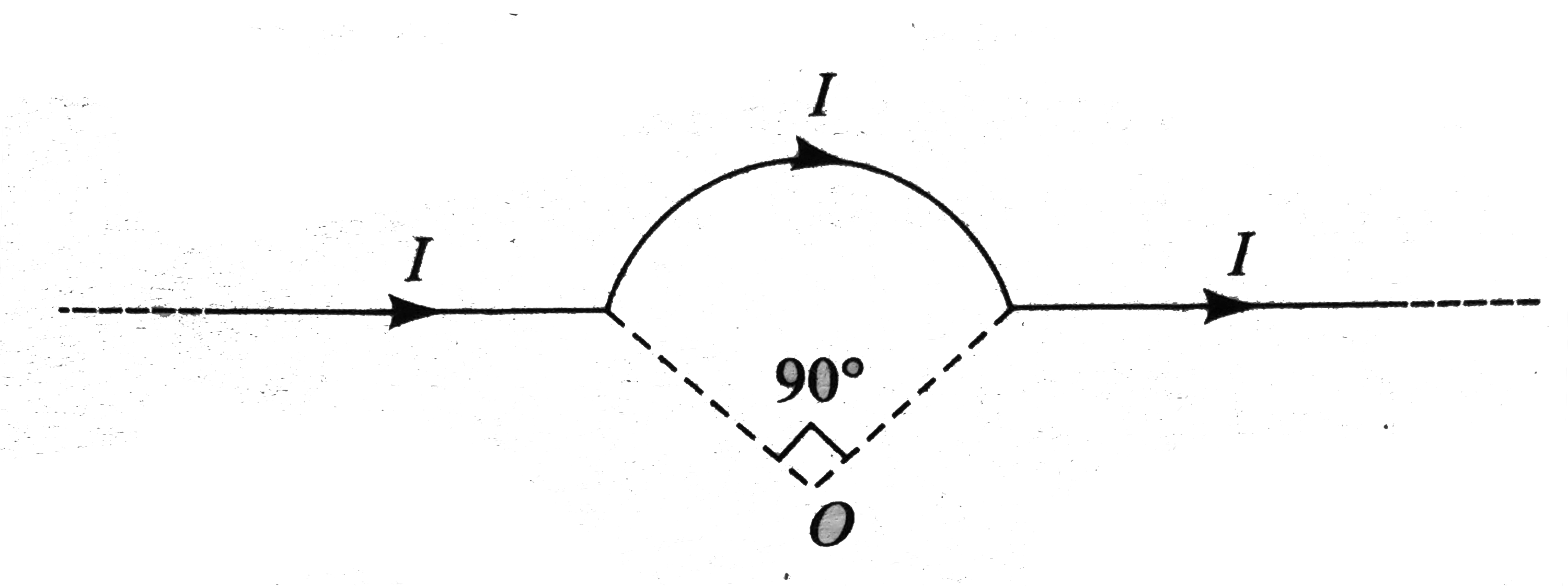
View SolutionThe magnetic field at centre O of the arc in Fig.
View SolutionIn a circle of radius 21 cm, an arc subtends an angle of 60o at the centre. Find: (i) length of the arc
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionIn a circle of radius 35 cm, an arc subtends an angle of 72o at the centre. Find the length of the arc and area of the sector.
View SolutionA battery is connected between two points AandB on the circumference of a uniform conducting ring of radius r and resistance R . One of the arcs AB of the ring subtends an angle θ at the centre . The value of the magnetic induction at the centre due to the current in the ring is
View Solution
