A horizontal wire carries 200A current below which another wire of linear density 20×10−3 Kg/m carrying a current is kept at 2cm distance. If the wire kept below hangs in air, then the current in the wire is
9.8 A
98 A
980 A
9800 A
The correct Answer is:B
To solve the problem, we need to find the current I2 in the second wire that is hanging in air. The forces acting on the second wire must be balanced, meaning the upward magnetic force due to the first wire must equal the downward gravitational force acting on the second wire.
1. Identify the Forces Acting on the Second Wire:
- The downward force is the weight of the second wire, given by:
Fdown=mg
- The upward force is the magnetic force due to the first wire, given by:
Fup=μ0I1I2l2πr
where:
- μ0=4π×10−7T m/A (permeability of free space)
- I1=200A (current in the first wire)
- I2 is the current in the second wire
- l is the length of the wire (assumed to be the same for both wires)
- r=2cm=0.02m (distance between the wires)
2. Set Up the Equation for Force Balance:
Since the forces are balanced, we can set them equal to each other:
mg=μ0I1I2l2πr
3. Express Mass in Terms of Linear Density:
The mass m of the second wire can be expressed in terms of its linear density λ:
m=λl
where λ=20×10−3kg/m.
4. Substituting Mass into the Force Balance Equation:
Substitute m into the force balance equation:
λlg=μ0I1I2l2πr
5. Cancel l from Both Sides:
Since l appears on both sides, we can cancel it out:
λg=μ0I1I22πr
6. Rearranging the Equation to Solve for I2:
Rearranging gives:
I2=2πrλgμ0I1
7. Substituting Known Values:
- r=0.02m
- λ=20×10−3kg/m
- g=9.8m/s2
- μ0=4π×10−7T m/A
- I1=200A
Plugging in these values:
I2=2π(0.02)(20×10−3)(9.8)4π×10−7×200
8. Simplifying the Expression:
- The π cancels out:
I2=2(0.02)(20×10−3)(9.8)4×10−7×200
- Simplifying further:
I2=0.0008×9.88×10−5=7.84×10−38×10−5=98A
Final Answer:
The current in the second wire I2 is 98A.
---
- The downward force is the weight of the second wire, given by:
Fdown=mg
- The upward force is the magnetic force due to the first wire, given by:
Fup=μ0I1I2l2πr
where:
- μ0=4π×10−7T m/A (permeability of free space)
- I1=200A (current in the first wire)
- I2 is the current in the second wire
- l is the length of the wire (assumed to be the same for both wires)
- r=2cm=0.02m (distance between the wires)
Since the forces are balanced, we can set them equal to each other:
mg=μ0I1I2l2πr
The mass m of the second wire can be expressed in terms of its linear density λ:
m=λl
where λ=20×10−3kg/m.
Substitute m into the force balance equation:
λlg=μ0I1I2l2πr
Since l appears on both sides, we can cancel it out:
λg=μ0I1I22πr
Rearranging gives:
I2=2πrλgμ0I1
- r=0.02m
- λ=20×10−3kg/m
- g=9.8m/s2
- μ0=4π×10−7T m/A
- I1=200A
I2=2π(0.02)(20×10−3)(9.8)4π×10−7×200
- The π cancels out:
I2=2(0.02)(20×10−3)(9.8)4×10−7×200
- Simplifying further:
I2=0.0008×9.88×10−5=7.84×10−38×10−5=98A
The current in the second wire I2 is 98A.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
Given below find the current in the wire BD.
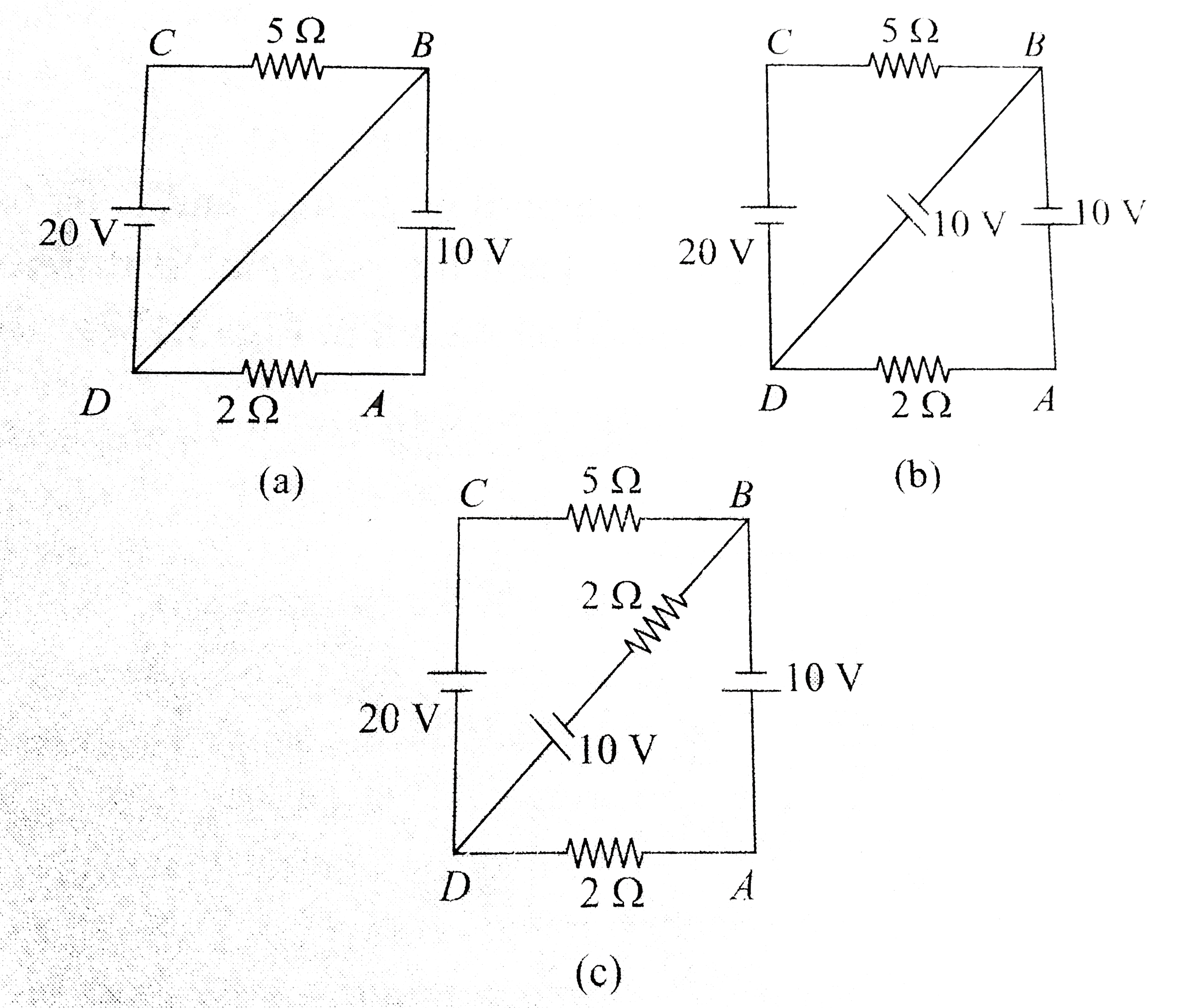 View Solution
View SolutionA fixed horizontal wire carries a current of 200 A. Another wire having a mass per unit length 10−2 kg/m is placed below the first wire at a distance of 2 cm and parallel to is. How much current must be passed through the second wire if it floats in air without any support? What should be the direction of current in it?
View SolutionA long straight wire is carrying a current of 25 A. A squre loop of side length 10 cm carrying a current of 15 A, is placed 2 cm from the wire as shown in figure. The force on the loop is
 View Solution
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionAn element has a face-centred cubic (fcc) structure with a cell edge of a. The distance between the centres of two nearest tetrahedral voids in the lattice is:
View SolutionIn the below circuit , AB is a wire of length 100 cm with 5Ω resistance . If there is no deflection in the galvanometer , the current flowing in the wire AB is
 View Solution
View SolutionA current carrying wire is placed below a coil in its plane, with current flowing as shown. If the current increases.
 View Solution
View SolutionA straight wilre of diameter 0.5mm carrying a current 2A is replaced by another wire of diameter 1mm carrying the same current. The strength of magnetic field at a distance 2m away from the centre is
View SolutionA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA straight , long wire carries a current a current of 20A. Another wire carrying equal current is placed parallel to it. If the force acting on a length of 10cm of the second wire is (2.0×(10−5))N, what is the separation between them?
View Solution

