If θcin the critical angle, write the deviation value when the ray travels from denser to rarer for i>θc.
To solve the problem, we need to determine the angle of deviation when a ray of light travels from a denser medium to a rarer medium, specifically when the angle of incidence i is greater than the critical angle θc.
1. Understanding the Critical Angle:
- The critical angle θc is defined as the angle of incidence above which total internal reflection occurs when light travels from a denser medium to a rarer medium.
2. Condition Given:
- We are given that the angle of incidence i is greater than the critical angle θc (i.e., i>θc). This means that total internal reflection will occur.
3. Total Internal Reflection:
- When total internal reflection occurs, the light ray does not pass into the rarer medium but instead reflects back into the denser medium. The angle of reflection r is equal to the angle of incidence i (i.e., r=i).
4. Angle of Deviation:
- The angle of deviation δ is defined as the angle between the incident ray and the emergent ray (which, in this case, is the reflected ray).
- The angle of deviation can be calculated using the formula:
δ=Incident Angle−Reflected Angle
- Since the angle of reflection is equal to the angle of incidence, we can express the angle of deviation as:
δ=i−r=i−i=0
- However, we need to consider the geometry of the situation. The angle between the incident ray and the reflected ray can be expressed as:
δ=π−2i
- This is because the total angle around the normal at the point of incidence sums up to π radians (or 180 degrees).
5. Final Expression:
- Therefore, when i>θc, the angle of deviation δ is given by:
δ=π−2i
Summary:
The angle of deviation when the ray travels from a denser medium to a rarer medium, with an angle of incidence greater than the critical angle, is given by:
δ=π−2i
- The critical angle θc is defined as the angle of incidence above which total internal reflection occurs when light travels from a denser medium to a rarer medium.
- We are given that the angle of incidence i is greater than the critical angle θc (i.e., i>θc). This means that total internal reflection will occur.
- When total internal reflection occurs, the light ray does not pass into the rarer medium but instead reflects back into the denser medium. The angle of reflection r is equal to the angle of incidence i (i.e., r=i).
- The angle of deviation δ is defined as the angle between the incident ray and the emergent ray (which, in this case, is the reflected ray).
- The angle of deviation can be calculated using the formula:
δ=Incident Angle−Reflected Angle
- Since the angle of reflection is equal to the angle of incidence, we can express the angle of deviation as:
δ=i−r=i−i=0
- However, we need to consider the geometry of the situation. The angle between the incident ray and the reflected ray can be expressed as:
δ=π−2i
- This is because the total angle around the normal at the point of incidence sums up to π radians (or 180 degrees).
- Therefore, when i>θc, the angle of deviation δ is given by:
δ=π−2i
The angle of deviation when the ray travels from a denser medium to a rarer medium, with an angle of incidence greater than the critical angle, is given by:
δ=π−2i
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-I)57videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS )24videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - PRACTICAL PHYSICSEXERCISE - LECTURE SHEET LEVEL-II (ADVANCED) Linked Comprehension Type Questions4videos
PRACTICAL PHYSICS
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III3videos
SEMICONDUCTOR DEVICES
Similar Questions
When a wave travels from a denser to rarer medium, then
View SolutionState whether the following statement is true or false ? If the angle of incidence is greater than the critical angle, light is not refracted at all, when it falls on the surface from a denser medium to a rarer medium.
View Solution
Knowledge Check
- Question 1 - Select One
When a light ray enters from a denser medium to a rarer medium.
AThe light ray bends towards the normal.BAngle of incidence is less than angle of refraction.CSpeed of light decreases.DSpeed of light remains unchanged.
Let the refractive index of a denser medium with respect to a rarer medium be n12 and its critical angle be θc. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90∘, Angle A given by -
View SolutionLet the refractive index of a denser medium with respect to a rarer medium be n12 and its critical angle be θc. At an angle of incidence A when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is 90∘, Angle A given by -
View SolutionFind the angle θa made by the light ray when it gets refracted from water to air, as shown in Fig .
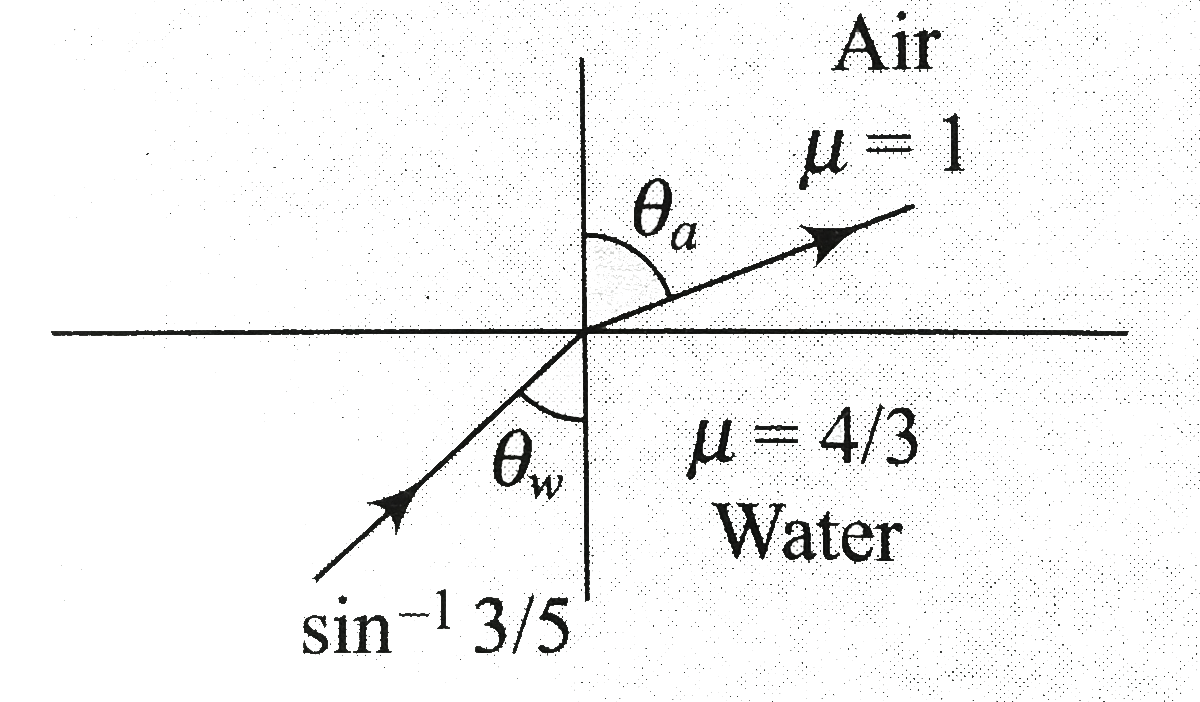 View Solution
View Solution(I) How does the refractive index of a medium depends on the wavelength of light used?
(II)Which is greater, angle of incidence or angle of refraction, when light travels from denser medium to rarer medium.View SolutionFill the blanks to complete the following sentence:
Q: When light travels from a denser to a rarer medium, its speed ______View SolutionSTATEMENT -1 : The critical angle is defined when light goes from denser medium to the rarer medium.
and
STATEMENT - 2 : In total internal reflection, intensity of light remains same.View SolutionStatement I: A ray is incident from outside on a glass sphere surrounded by air as shown in Figure. This ray may suffer total internal reflection at the second interface.

Statement II: For a ray going from a denser to rarer medium, the ray may suffer total internal reflection.View Solution

