Two capacitors of capacity 4μFand6μF are connected in series and a battery is connected to the combination. The energy stored is E1 If they are connected in parallel and if the same battery is connected to this combination the energy stored is E2 The ratio E1:E2 is
A) 4:9
B) 9:14
C) 6:25
D) 7:12
The correct Answer is:C
To solve the problem, we need to calculate the energy stored in two capacitors when they are connected in series and in parallel, and then find the ratio of these energies.
1. Identify the given values:
- Capacitor 1, C1=4μF
- Capacitor 2, C2=6μF
- Let the voltage of the battery be V.
2. Calculate the equivalent capacitance when capacitors are connected in series:
The formula for the equivalent capacitance Cs of capacitors in series is:
1Cs=1C1+1C2
Substituting the values:
1Cs=14+16
Finding a common denominator (which is 12):
1Cs=312+212=512
Therefore,
Cs=125μF=2.4μF
3. Calculate the energy stored in the series configuration E1:
The energy stored in a capacitor is given by:
E=12CV2
Thus, for the series configuration:
E1=12CsV2=12×2.4μF×V2
4. Calculate the equivalent capacitance when capacitors are connected in parallel:
The formula for the equivalent capacitance Cp of capacitors in parallel is:
Cp=C1+C2
Substituting the values:
Cp=4μF+6μF=10μF
5. Calculate the energy stored in the parallel configuration E2:
Thus, for the parallel configuration:
E2=12CpV2=12×10μF×V2
6. Find the ratio E1:E2:
Now we can find the ratio of the energies:
E1E2=12×2.4μF×V212×10μF×V2
The 12 and V2 cancel out:
E1E2=2.4μF10μF=2.410=625
7. Final Answer:
Thus, the ratio E1:E2 is:
E1:E2=6:25
- Capacitor 1, C1=4μF
- Capacitor 2, C2=6μF
- Let the voltage of the battery be V.
The formula for the equivalent capacitance Cs of capacitors in series is:
1Cs=1C1+1C2
Substituting the values:
1Cs=14+16
Finding a common denominator (which is 12):
1Cs=312+212=512
Therefore,
Cs=125μF=2.4μF
The energy stored in a capacitor is given by:
E=12CV2
Thus, for the series configuration:
E1=12CsV2=12×2.4μF×V2
The formula for the equivalent capacitance Cp of capacitors in parallel is:
Cp=C1+C2
Substituting the values:
Cp=4μF+6μF=10μF
Thus, for the parallel configuration:
E2=12CpV2=12×10μF×V2
Now we can find the ratio of the energies:
E1E2=12×2.4μF×V212×10μF×V2
The 12 and V2 cancel out:
E1E2=2.4μF10μF=2.410=625
Thus, the ratio E1:E2 is:
E1:E2=6:25
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )108videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Two capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionFigure shows two capacitors of capacitance 2μF and 4μF and a cell of 90 V. The switch 'k' is such that when it is in position 1, the circuit ABCD is closed and when it is in position 2, the circuit BCEF is closed.the resistance of both the circuits is negligible os that the capacitor gets fully charged instantly. Initially the switch is in position1. then it is turned in position 2 and then in position 1. Now two cycles are completed. Find the charge (inμC) after two cycles.
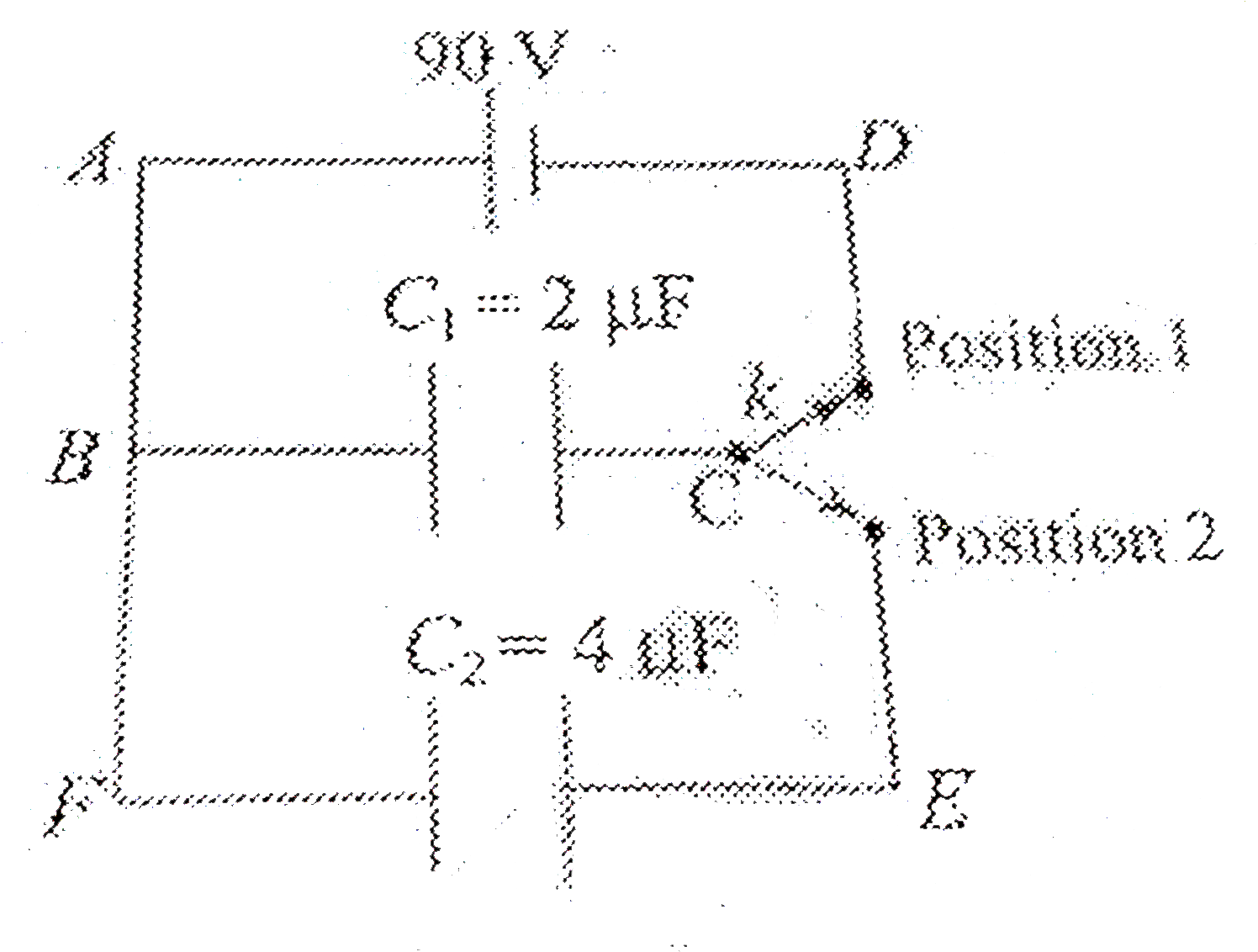 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The potential difference between points A and B is
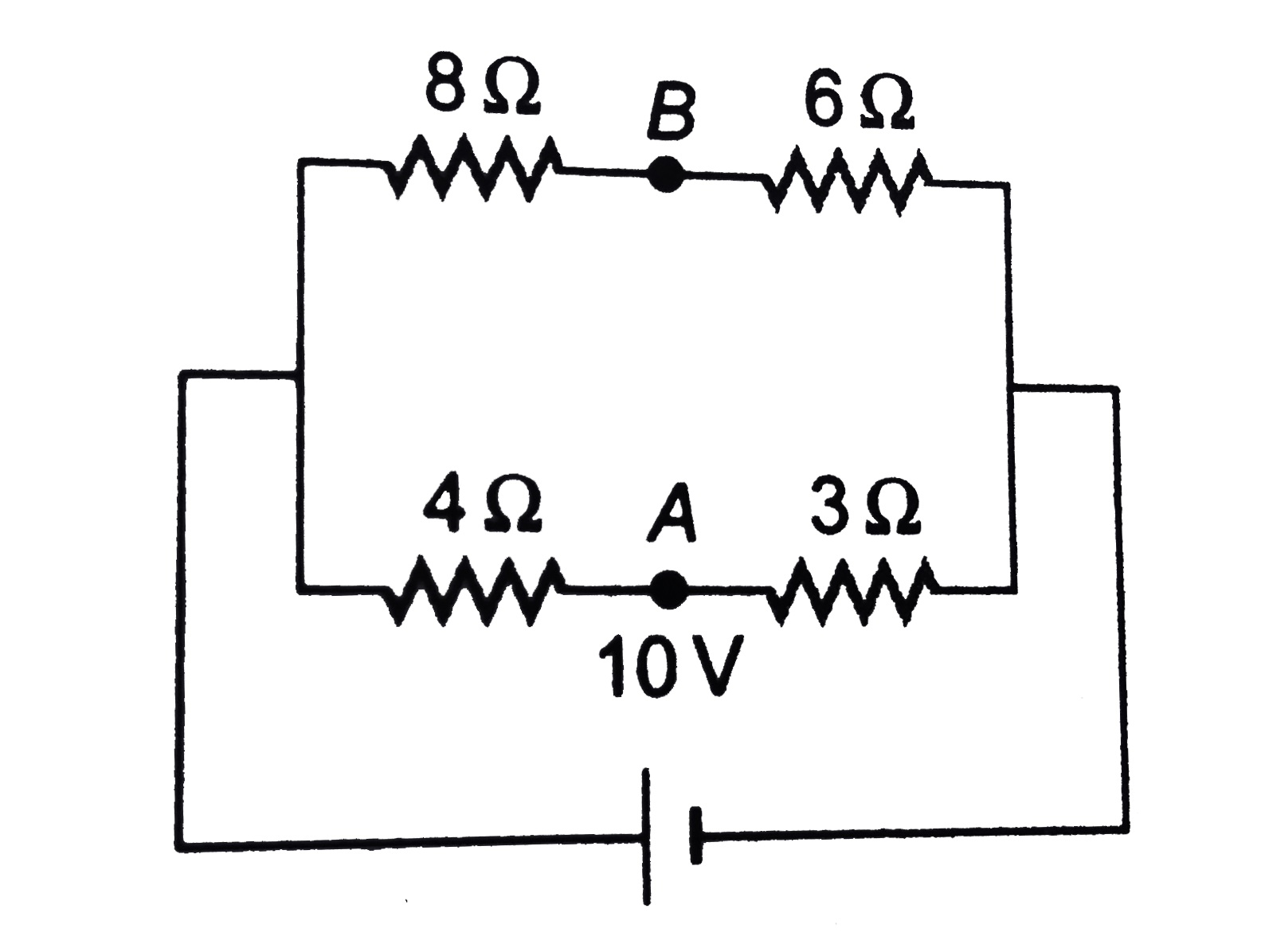 A2B5C11D18
A2B5C11D18 - Question 2 - Select One
Two capacitrors of 2μFand4μF are connected in parallel. A third capacitor of 6μF is connected in series. The combaination is connected across a 12 V battery. The voltage across 2μF capacitor is
A2 VB8 VC6 VD1 V
Three capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionA capacitor of capacitance 6 μF is connected with an emf sourface 3 V. Electrostaci energy stored in the capacitor is
View SolutionTwo condensers of capacity 0.3μF and 0.6μF respectively are connected in series. The combination is connected across a potential of 6 volts. The ratio of energies stored by the condensers will be
View SolutionThree condensers of same capacity connected in series has effective capacity 2mF. If they are connected in parallel and charged using a battery of emf 12V, the total energy stored in the combination is
View SolutionTwo identical capacitors of 12pF each are connected in a series across a battery of 50V. How much electrostatic energy is stored in the combination ? If these were connected in parallel across the same battery , how much energy will be stored in combintion now ?
Also find the charge drawn from the battery in each case.View SolutionThree capacitors of capacitances 2μF, 3μF and 6μF are connected in series with a 12 V battery. All the connecting wire are disconnected, the three positive plates are connected together and the three negative plates are connected together. Find the charges on the three capacitors after the reconnection.
View Solution
