A parallel plate capacitor is filled with a dielectric of dielectric constant (relative permittivity) 5 between its plates and is charged to acquire an energy E. Then it is isolated (disconnected from the battery) and the dielectric is replaced by another dielectric of dielectric constant (relative permittivity) 2. The new energy stored in the capacitor
A) E
B) 2.5E
C) 5E
D) 10E
The correct Answer is:B
To solve the problem, we need to analyze the situation of a parallel plate capacitor filled with different dielectrics and how the energy stored in the capacitor changes when the dielectric is replaced.
1. Understand the Initial Conditions:
- Let C0 be the capacitance of the capacitor when it is filled with air (no dielectric).
- When a dielectric with dielectric constant k1=5 is inserted, the new capacitance C1 becomes:
C1=k1C0=5C0
2. Calculate the Initial Energy Stored:
- The energy E stored in the capacitor when filled with the dielectric of constant k1 is given by:
E=Q22C1
- Here, Q is the charge on the capacitor, which remains constant since the capacitor is isolated.
3. Relate Energy to Capacitance:
- The energy can also be expressed in terms of the initial capacitance C0:
E=Q22(5C0)=Q210C0
4. Introduce the New Dielectric:
- Now, the dielectric is replaced with another dielectric of constant k2=2. The new capacitance C2 becomes:
C2=k2C0=2C0
5. Calculate the New Energy Stored:
- The new energy E′ stored in the capacitor with the new dielectric is given by:
E′=Q22C2=Q22(2C0)=Q24C0
6. Relate the New Energy to the Initial Energy:
- Now we can relate E′ to E:
E′=Q24C0=Q210C0⋅104=E⋅104=2.5E
7. Final Result:
- Therefore, the new energy stored in the capacitor after replacing the dielectric is:
E′=2.5E
Conclusion:
The new energy stored in the capacitor is 2.5E, which corresponds to option B.
- Let C0 be the capacitance of the capacitor when it is filled with air (no dielectric).
- When a dielectric with dielectric constant k1=5 is inserted, the new capacitance C1 becomes:
C1=k1C0=5C0
- The energy E stored in the capacitor when filled with the dielectric of constant k1 is given by:
E=Q22C1
- Here, Q is the charge on the capacitor, which remains constant since the capacitor is isolated.
- The energy can also be expressed in terms of the initial capacitance C0:
E=Q22(5C0)=Q210C0
- Now, the dielectric is replaced with another dielectric of constant k2=2. The new capacitance C2 becomes:
C2=k2C0=2C0
- The new energy E′ stored in the capacitor with the new dielectric is given by:
E′=Q22C2=Q22(2C0)=Q24C0
- Now we can relate E′ to E:
E′=Q24C0=Q210C0⋅104=E⋅104=2.5E
- Therefore, the new energy stored in the capacitor after replacing the dielectric is:
E′=2.5E
The new energy stored in the capacitor is 2.5E, which corresponds to option B.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (CUTTENT ELECTRICITY )108videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Knowledge Check
- Question 1 - Select One
A parallel plate air capacitor has a capacitance C. When it is half filled with a dielectric of dielectric constant 5, the percentage increase in the capacitance will be
A400%B66.6%C33.3%D200%
A parallel plate capacitor has a dielectric (of dielectric constant k) between the plates. The plates are charged to a surface charge density σ0. What is the density of the polarized charge that appear on the surface of the dielectric.
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be
 View Solution
View SolutionA parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
View SolutionA parallel plate capacitor is half filled with a dielectric slab of dielectric constant (K) and mass M. Capacitor is connected to a cell of e.m.f. E. Plates are held fixed on horizontal surface. A bullet of mass M hits the dielectric elastically and it is found that the dielectric slab just leaves out the capacitor. Find the speed of the bullet?
 View Solution
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
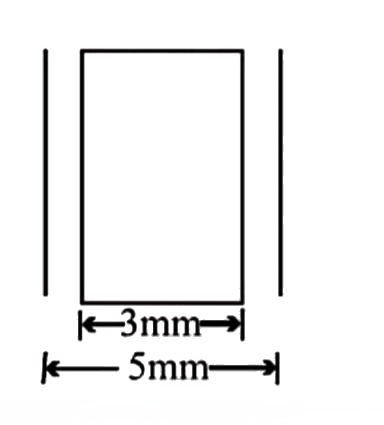 View Solution
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
View SolutionA parallel plate capacitor with square plates is filed with four dielectrics of dielectric constants K1,K2,K3,K4, arranged as shown in the figure. The effective dielectric constant K will be :
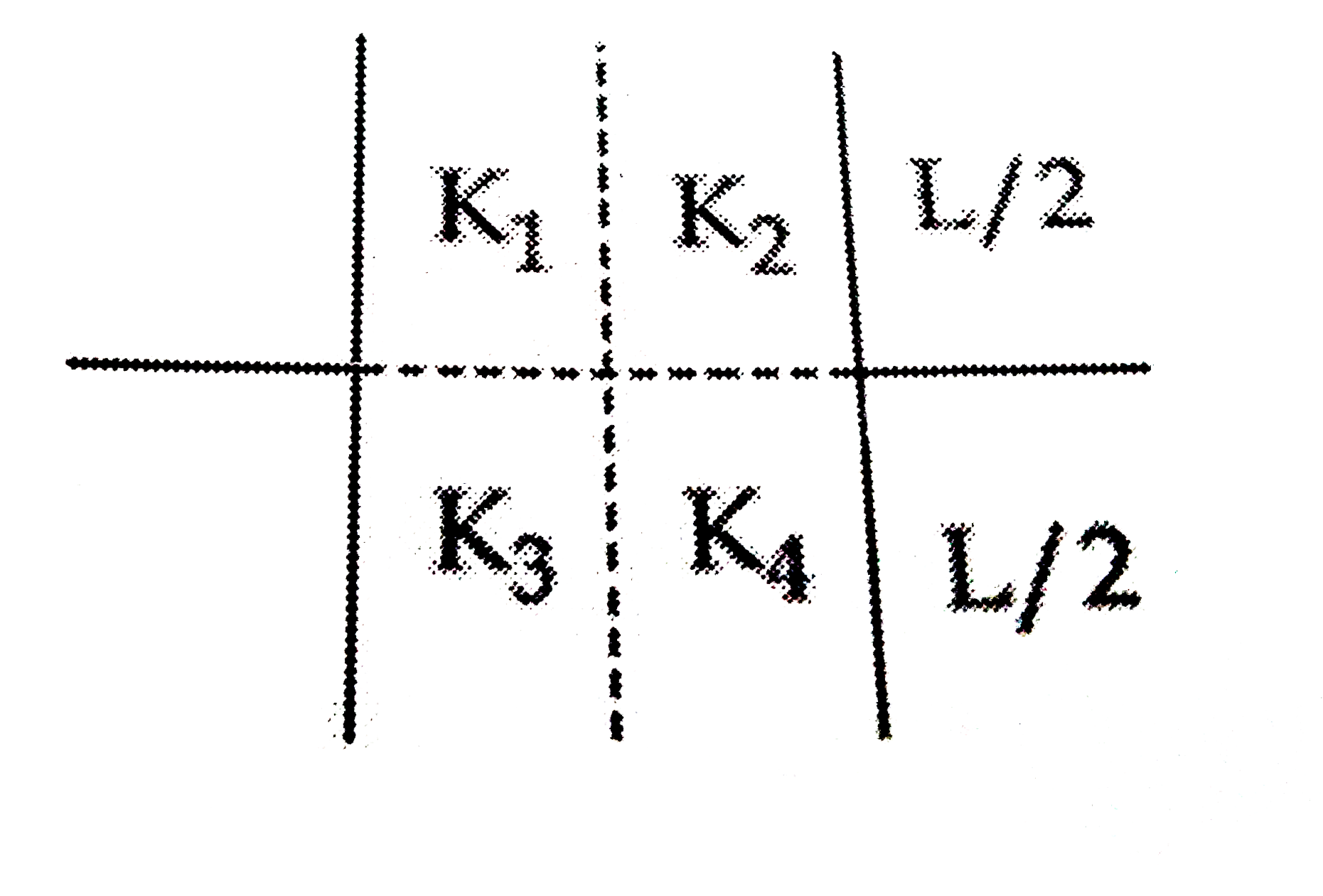 View Solution
View Solution
