A dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is and the magnitude of the induced charge on each surface of the dielectric is .
Q' may be larger than Q.
Q' must be larger than Q.
Q' must be equal to Q.
Q'must be smaller tha Q.
The correct Answer is:D
To solve the problem, we need to analyze the situation of a parallel plate capacitor with a dielectric slab inserted between its plates. The charge on the capacitor is Q, and we want to determine the relationship between the charge Q′ induced on the surfaces of the dielectric slab and the charge Q on the capacitor.
1. Understanding the Setup:
- We have a parallel plate capacitor with charge Q on one plate and −Q on the other plate.
- When a dielectric slab with dielectric constant K is inserted, it affects the electric field between the plates.
2. Electric Field Without Dielectric:
- The electric field E0 in the absence of the dielectric is given by:
E0=QAϵ0
where A is the area of the plates and ϵ0 is the permittivity of free space.
3. Electric Field With Dielectric:
- When the dielectric is inserted, the electric field E becomes:
E=QAϵ0K
This is because the dielectric reduces the electric field by a factor of K.
4. Induced Charge on the Dielectric:
- The dielectric slab will have induced charges on its surfaces due to the electric field. The charge induced on the positive surface of the dielectric is Q′.
5. Relation Between Charges:
- The induced charge Q′ can be related to the electric field due to polarization. The electric field due to the induced charge is:
Ep=Q′Aϵ0
- The net electric field E between the plates can be expressed as:
E=E0−Ep
6. Setting Up the Equation:
- Substituting the expressions for E0 and Ep:
QAϵ0K=QAϵ0−Q′Aϵ0
- Multiplying through by Aϵ0 to eliminate the denominators:
QK=Q−Q′
7. Solving for Induced Charge Q′:
- Rearranging the equation gives:
Q′=Q−QK
- Factoring out Q:
Q′=Q(1−1K)
8. Analyzing the Result:
- Since K>1 (the dielectric constant is always greater than 1), the term (1−1K) is positive but less than 1. Therefore:
Q′<Q
Conclusion:
The induced charge Q′ on each surface of the dielectric slab must be smaller than the charge Q on the capacitor. Thus, the correct answer is that Q′ must be smaller than Q.
- We have a parallel plate capacitor with charge Q on one plate and −Q on the other plate.
- When a dielectric slab with dielectric constant K is inserted, it affects the electric field between the plates.
- The electric field E0 in the absence of the dielectric is given by:
E0=QAϵ0
where A is the area of the plates and ϵ0 is the permittivity of free space.
- When the dielectric is inserted, the electric field E becomes:
E=QAϵ0K
This is because the dielectric reduces the electric field by a factor of K.
- The dielectric slab will have induced charges on its surfaces due to the electric field. The charge induced on the positive surface of the dielectric is Q′.
- The induced charge Q′ can be related to the electric field due to polarization. The electric field due to the induced charge is:
Ep=Q′Aϵ0
- The net electric field E between the plates can be expressed as:
E=E0−Ep
- Substituting the expressions for E0 and Ep:
QAϵ0K=QAϵ0−Q′Aϵ0
- Multiplying through by Aϵ0 to eliminate the denominators:
QK=Q−Q′
- Rearranging the equation gives:
Q′=Q−QK
- Factoring out Q:
Q′=Q(1−1K)
- Since K>1 (the dielectric constant is always greater than 1), the term (1−1K) is positive but less than 1. Therefore:
Q′<Q
The induced charge Q′ on each surface of the dielectric slab must be smaller than the charge Q on the capacitor. Thus, the correct answer is that Q′ must be smaller than Q.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Objective 1
12 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionWhen a dielectric slab is gradually inserted between the plates of an isolated parallel-plate capacitor , the energy of the system decreases.What can you conclude about the force on the slab exerted by the electric field?
View SolutionA dielectric slab is inserted between the plates of an isolatted charged capacitor. Which of the following quantities will remain the same?
View SolutionOn placing dielectric slab between the plates of an isolated charged condenser its
View SolutionAssertion: A dielectric slabis inserted between plates of an isolated capacitor. charge on capacitor will remain same.
Reason Charge on an isolated system is conserved.
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
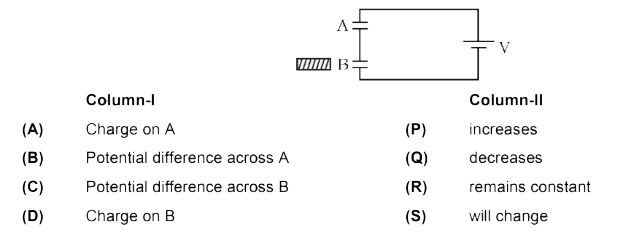
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors in figure , which of the following properties increase ?
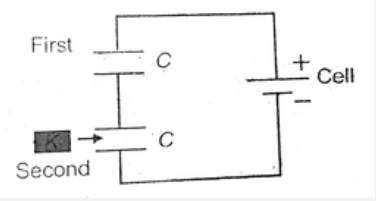
View SolutionA parallel plate capacitor has a dielectric (of dielectric constant k) between the plates. The plates are charged to a surface charge density σ0. What is the density of the polarized charge that appear on the surface of the dielectric.
View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solution
