A magnet of length 10cm and magnetic moment 1 Am2 is placed along the side AB of an equilateral triangle ABC. If the length of the side AB is 10cm, the magnetic induction at the point C is
10−9T
10−7T
10−5T
10−4T
To solve the problem of finding the magnetic induction at point C due to a magnet placed along side AB of an equilateral triangle ABC, we can follow these steps:
1. Understand the Geometry:
- We have an equilateral triangle ABC with each side measuring 10 cm.
- The magnet is placed along side AB.
2. Identify the Magnetic Moment:
- The magnetic moment m of the magnet is given as 1Am2.
3. Convert Units:
- Convert the length of the sides from centimeters to meters for consistency in SI units:
L=10cm=0.1m
4. Calculate the Distance from the Magnet to Point C:
- In an equilateral triangle, the height h can be calculated using the formula:
h=√32L=√32×0.1≈0.0866m
- The distance from the midpoint of AB to point C is h.
5. Use the Magnetic Induction Formula:
- The magnetic induction B at a point due to a magnetic dipole is given by:
B=μ04π⋅2mr3
- Here, μ0 (permeability of free space) is 4π×10−7T m/A, and r is the distance from the magnet to point C.
6. Substitute Values:
- Substitute m=1Am2 and r=0.0866m:
B=4π×10−74π⋅2⋅1(0.0866)3
- Simplifying gives:
B=10−7⋅2(0.0866)3
7. Calculate (0.0866)3:
- Calculate (0.0866)3≈0.000650.
8. Final Calculation:
- Now substitute back:
B=10−7⋅20.000650≈10−7⋅3076.92≈3.08×10−4T
Conclusion:
The magnetic induction at point C is approximately 3.08×10−4T.
- We have an equilateral triangle ABC with each side measuring 10 cm.
- The magnet is placed along side AB.
- The magnetic moment m of the magnet is given as 1Am2.
- Convert the length of the sides from centimeters to meters for consistency in SI units:
L=10cm=0.1m
- In an equilateral triangle, the height h can be calculated using the formula:
h=√32L=√32×0.1≈0.0866m
- The distance from the midpoint of AB to point C is h.
- The magnetic induction B at a point due to a magnetic dipole is given by:
B=μ04π⋅2mr3
- Here, μ0 (permeability of free space) is 4π×10−7T m/A, and r is the distance from the magnet to point C.
- Substitute m=1Am2 and r=0.0866m:
B=4π×10−74π⋅2⋅1(0.0866)3
- Simplifying gives:
B=10−7⋅2(0.0866)3
- Calculate (0.0866)3≈0.000650.
- Now substitute back:
B=10−7⋅20.000650≈10−7⋅3076.92≈3.08×10−4T
The magnetic induction at point C is approximately 3.08×10−4T.
Topper's Solved these Questions
- APPENDICES ( REVISION EXERCISE )BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)
95 Videos
- ALTERNATING CURRENTBOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III
24 Videos
- APPENDICES (REVISION EXERCISE)BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION
128 Videos
Similar Questions
Knowledge Check
In the figure, if AB = 10, what is the length of the side CD ?
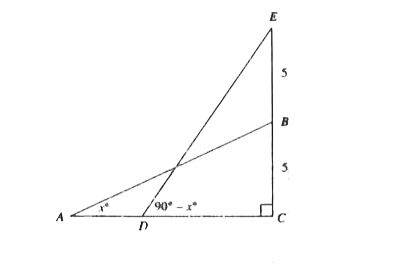 A5B5√3C10√3D10
A5B5√3C10√3D10
A current of 2A is flowing in the sides of an equilateral triangle of side 9 cm. The magnetic field at the centroid of the triangle is
View SolutionEach side of an equilateral triangle measure 10 cm. Find the area of the triangle .
View SolutionConstruct on equilateral triangle each of whose sides is of length 4.6cm.
View SolutionThe current I ampere is flowing in an equilateral triangle of side a the magnetic field induction at the centroid will be
View SolutionA current of 1⋅0A flowing in the sides of an equilateral triangle of side 4⋅5×10−2m. Find the magnetic fied at the centroid of the triangle.
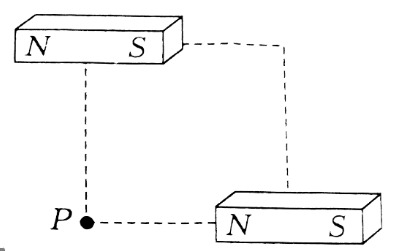
View SolutionTwo short magnets of magnetic moment 1000Am2 are placed as shown at the corners of a square of side 10cm. The net magnetic induction at P is
View SolutionThe sides of an equilateral triangle are increasing at the rate of 2 cm/sec. How far is the area increasing when the side is 10 cms?
View Solution
