Two magnets of moments M1andM2 are rigidly fixed together at their centres so that their axes are inclined to each other. This system is suspended in a magnetic field of induction 'B' so that M1 makes an angles θ1 and M2 makes an angles θ2 with the field direction and unlike poles on either side of the field direction. The resultant torque on the rigid system is
A) B(M1sinθ1+M2sinθ2)
B) B(M1cosθ1+M2cosθ2)
C) B(M1sinθ2+M2sinθ1)
D) B(M1cosθ2+M2cosθ1)
To find the resultant torque on the rigid system of two magnets, we can follow these steps:
Step 1: Understand the Torque on a Single Magnet
The torque (τ) acting on a magnet with magnetic moment M in a magnetic field B is given by the formula:
τ=M×B
For the magnitude of the torque, we can express it as:
τ=MBsinθ
where θ is the angle between the magnetic moment and the magnetic field.
Step 2: Apply the Torque Formula to Each Magnet
Since we have two magnets with moments M1 and M2, and they make angles θ1 and θ2 with the magnetic field respectively, we can write the torques for each magnet:
- For magnet 1:
τ1=M1Bsinθ1
- For magnet 2:
τ2=M2Bsinθ2
Step 3: Calculate the Resultant Torque
The total torque on the system is the vector sum of the individual torques. Since the magnets are fixed together and their axes are inclined, the resultant torque (τ) can be expressed as:
τ=τ1+τ2
Substituting the expressions for τ1 and τ2:
τ=M1Bsinθ1+M2Bsinθ2
Step 4: Factor Out Common Terms
Since B is common in both terms, we can factor it out:
τ=B(M1sinθ1+M2sinθ2)
Final Result
Thus, the resultant torque on the rigid system of magnets is:
τ=B(M1sinθ1+M2sinθ2)
The torque (τ) acting on a magnet with magnetic moment M in a magnetic field B is given by the formula:
τ=M×B
For the magnitude of the torque, we can express it as:
τ=MBsinθ
where θ is the angle between the magnetic moment and the magnetic field.
Since we have two magnets with moments M1 and M2, and they make angles θ1 and θ2 with the magnetic field respectively, we can write the torques for each magnet:
- For magnet 1:
τ1=M1Bsinθ1
- For magnet 2:
τ2=M2Bsinθ2
The total torque on the system is the vector sum of the individual torques. Since the magnets are fixed together and their axes are inclined, the resultant torque (τ) can be expressed as:
τ=τ1+τ2
Substituting the expressions for τ1 and τ2:
τ=M1Bsinθ1+M2Bsinθ2
Since B is common in both terms, we can factor it out:
τ=B(M1sinθ1+M2sinθ2)
Thus, the resultant torque on the rigid system of magnets is:
τ=B(M1sinθ1+M2sinθ2)
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MOVING CHANGES & MEGNETISM)95videos
APPENDICES ( REVISION EXERCISE )
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - III24videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES (REVISION EXERCISE)EXERCISE - LAW OF MOTION128videos
APPENDICES (REVISION EXERCISE)
Similar Questions
Potential energy of a bar mangnet of magnetic moment M placed in a magnetic field of induction B such that it makes an angle θ with the direction of B is (take θ=90∘ as datum)
View SolutionTwo magnets of moment M and 2 M are tied at an angle of 60∘ to each other . What is the resultant magnetic moment of the combination ?
View SolutionTwo magnets of magnetic moments M and M√3 are joined to form a cross(+) . The combination is suspended freely in a uniform magnetic field . At equilibrium position, the magnet of magnetic moment M makes an angle theta with the field, then theta is
View SolutionThe length of a bar magnet is 10 cm and its pole strength is 10−3 Weber. It is placed in a magnetic field of induction 4π×10−3 Tesla in a direction making an angle 30∘ with the field direction. The value of torque acting on the magnet will be –
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
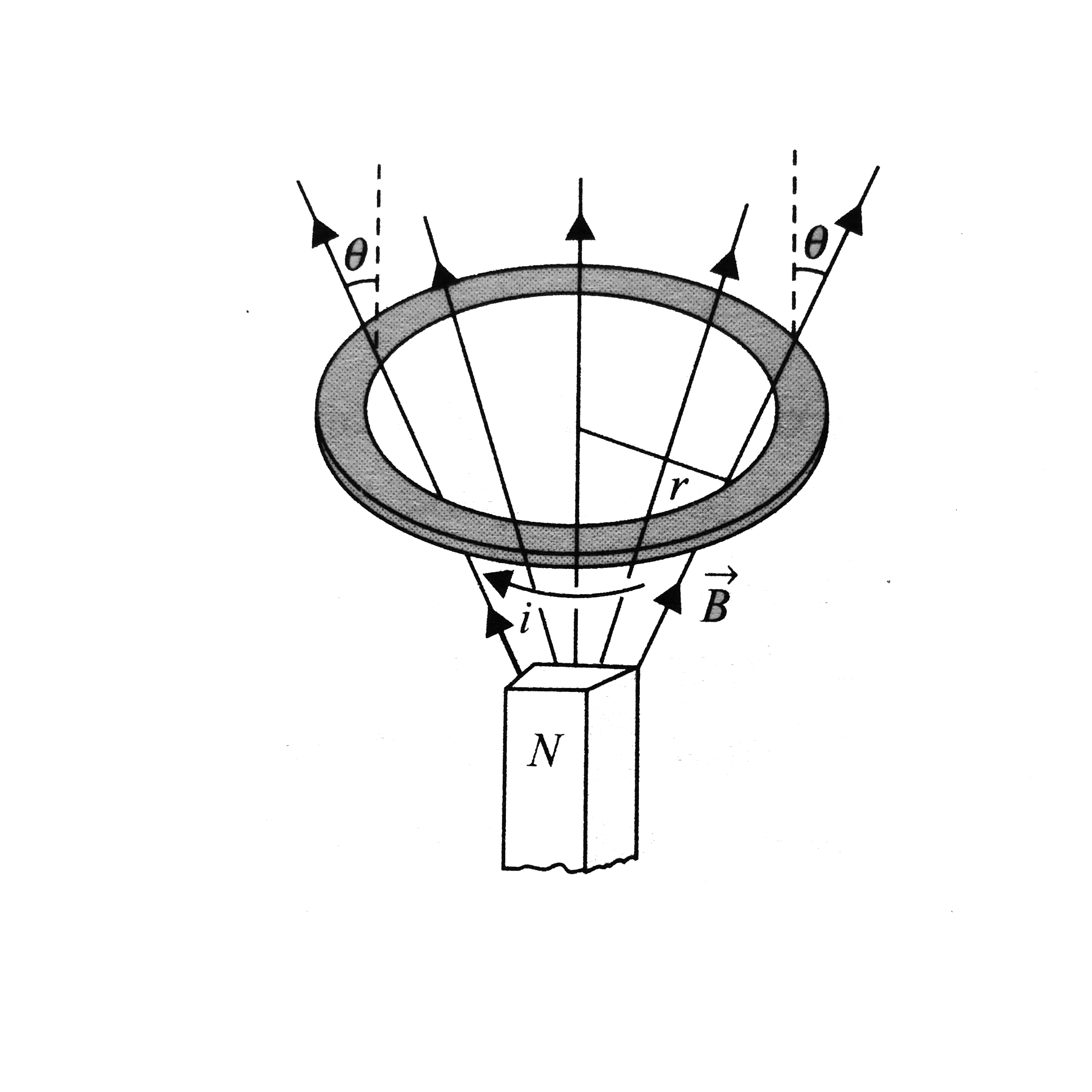 View Solution
View SolutionA bar magnet of magnetic moment →M is placed in a magnetic field of induction →B . The torque exerted on it is
View SolutionTwo magnets, each of magnetic miment 'M' are placed so as to form a cross at right angles to each other. The magnetic moment of the system will be
View SolutionThe rate of change of torque 'τ' with deflection θ is maximum for a magnet suspended freely in a uniform magnetic field of induction B when θ is equal to
View SolutionTwo vectors having equal magnitudes A make an angle θ with each other. Find the magnitude and direction of the resultant.
View SolutionIf a bar magnet moment M is freely suspended in a uniform magnetic field of strength field of strength B, then the work done in rotating the magent through an angle θ is
View Solution
