NAND and NOR gates are called universal gates primarily, because they
are available universally
can be combined to produce OR, AND and NOT gates
are widely used in integrated circuits
are easiest to manufacture
The correct Answer is:B
To solve the question regarding why NAND and NOR gates are called universal gates, we can break down the reasoning step by step.
1. Understanding Universal Gates:
- Universal gates are logic gates that can be used to create any other type of gate (AND, OR, NOT) through combinations of themselves.
2. Identifying NAND and NOR Gates:
- The NAND gate is a combination of an AND gate followed by a NOT operation.
- The NOR gate is a combination of an OR gate followed by a NOT operation.
3. Producing Other Gates:
- By using multiple NAND gates, we can create:
- An AND gate: By connecting two NAND gates in a certain configuration.
- An OR gate: By using NAND gates to create the equivalent of an OR function.
- A NOT gate: By connecting a single input to a NAND gate.
- Similarly, NOR gates can also be used to create AND, OR, and NOT gates.
4. Application in Integrated Circuits:
- NAND and NOR gates are widely used in digital electronics and integrated circuits. Their ability to be combined to form any other gate makes them very versatile and essential in circuit design.
5. Conclusion:
- The primary reason NAND and NOR gates are referred to as universal gates is because they can be combined to produce all other basic gates (AND, OR, NOT), and they are widely used in integrated circuits.
Final Answer:
NAND and NOR gates are called universal gates primarily because they can be combined to produce all other basic gates (AND, OR, NOT) and are widely used in integrated circuits.
- Universal gates are logic gates that can be used to create any other type of gate (AND, OR, NOT) through combinations of themselves.
- The NAND gate is a combination of an AND gate followed by a NOT operation.
- The NOR gate is a combination of an OR gate followed by a NOT operation.
- By using multiple NAND gates, we can create:
- An AND gate: By connecting two NAND gates in a certain configuration.
- An OR gate: By using NAND gates to create the equivalent of an OR function.
- A NOT gate: By connecting a single input to a NAND gate.
- Similarly, NOR gates can also be used to create AND, OR, and NOT gates.
- NAND and NOR gates are widely used in digital electronics and integrated circuits. Their ability to be combined to form any other gate makes them very versatile and essential in circuit design.
- The primary reason NAND and NOR gates are referred to as universal gates is because they can be combined to produce all other basic gates (AND, OR, NOT), and they are widely used in integrated circuits.
NAND and NOR gates are called universal gates primarily because they can be combined to produce all other basic gates (AND, OR, NOT) and are widely used in integrated circuits.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (MATCHING TYPE QUESTIONS)9videos
SEMICONDUCTOR DEVICES
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (MORE THAN ONE OPTION TYPE QUESTIONS)23videos
SEMICONDUCTOR DEVICES
- BOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE -I (TRANSISTORS)22videos
SEMICONDUCTOR DEVICES
- BOOK - AAKASH SERIESCHAPTER - RAY OPTICSEXERCISE - PROBLEMS ( LEVEL-II)60videos
RAY OPTICS
- BOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE45videos
UNITS AND MEASUREMENT
Similar Questions
Knowledge Check
- Question 1 - Select One
An AND gate
Ais equivalent to a parallel switching currentBis equivalent to a series switching currentChas two outputs and one inputsDhas two outputs and two inputs
Out of the following, universal gate is :-
View SolutionChlorophyll a is called universal photosynthetic pigment because it occurs in
View SolutionNAND gate is-
View SolutionWhich of the following pairs are universal gates
View SolutionThe minimum NOR gates are required to make one NAND gate are
View SolutionThe figure shows two NAND gates followed by a NOR gate. The system is equivalent to the following logic gate
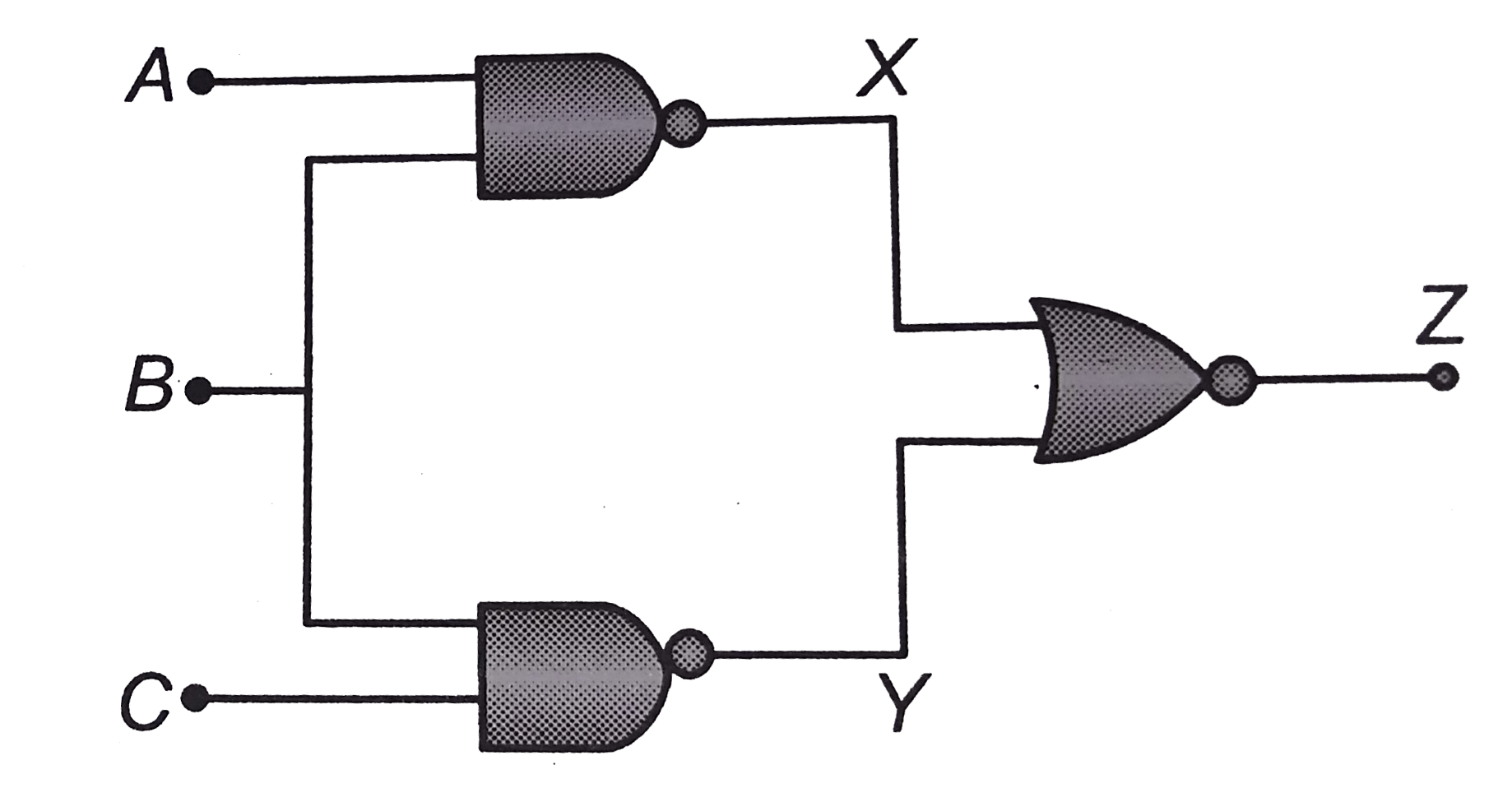 View Solution
View SolutionThe inputs A and B are inverted by using two NOT gates and their outputs are fed to the NOR gate as shown:
Analyse the action of the gates (1) and (2) and identify the logic gate of the complete circuit so obtained. Give its symbol and the truth table.
 View Solution
View Solution

