A thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity ω. Find the ratio of its magnetic moment and angular momentum.
ML=q2m
Topper's Solved these Questions
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE
13 Videos
- ELECTROMAGNETICSBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - PROBLEMS (LEVEL -I)
40 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - EXERCISE -II
22 Videos
- ELECTROSTATICSBOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
5 Videos
Similar Questions
A ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(iii)Magnetic moment of ring.
View SolutionA thin disc of radius R has charge Q distributed uniformly on its surface. The disc is rotated about one of its diametric axis with angular velocity ω. The magnetic moment of the arrangement is
View Solution
Knowledge Check
A solid cylinder of mass M and radius R rotates about its axis with angular speed ω. Its rotational kinetic energy is
A12MR2ω2BMR2ω2C14MR2ω2D18MR2ω2
A ring of mass m and radius R is being rotated about its axis with angular velocity o. If o increases then tension in ring
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(i)Current produced due to motion of ring
View SolutionSolid uniform conductiong sphere of mass 'm' and charge Q, rotates about its axis of symmetry with constant angular velocity 'ω' then the ratio of magnetic moment to the moment of inertia of the sphere is xQω6m then x is :(Neglect induced charges due to centrifugal force)
View SolutionA long cylinder of radius a carrying a uniform surface charge rotates about its axis with an angular velocity ω. Find the magnetic field energy per unit length of the cylinder if the linear charge density equals λ and μ=1.
View SolutionConsider a hypothetic spherical body. The body is cut into two parts about the diameter. One of hemispherical portion has mass distribution m while the other portion has indentical charge distribution q. The body is rotated about the axis with constant speed ω. Then, the ratio of magnetic moment to angular momentum is
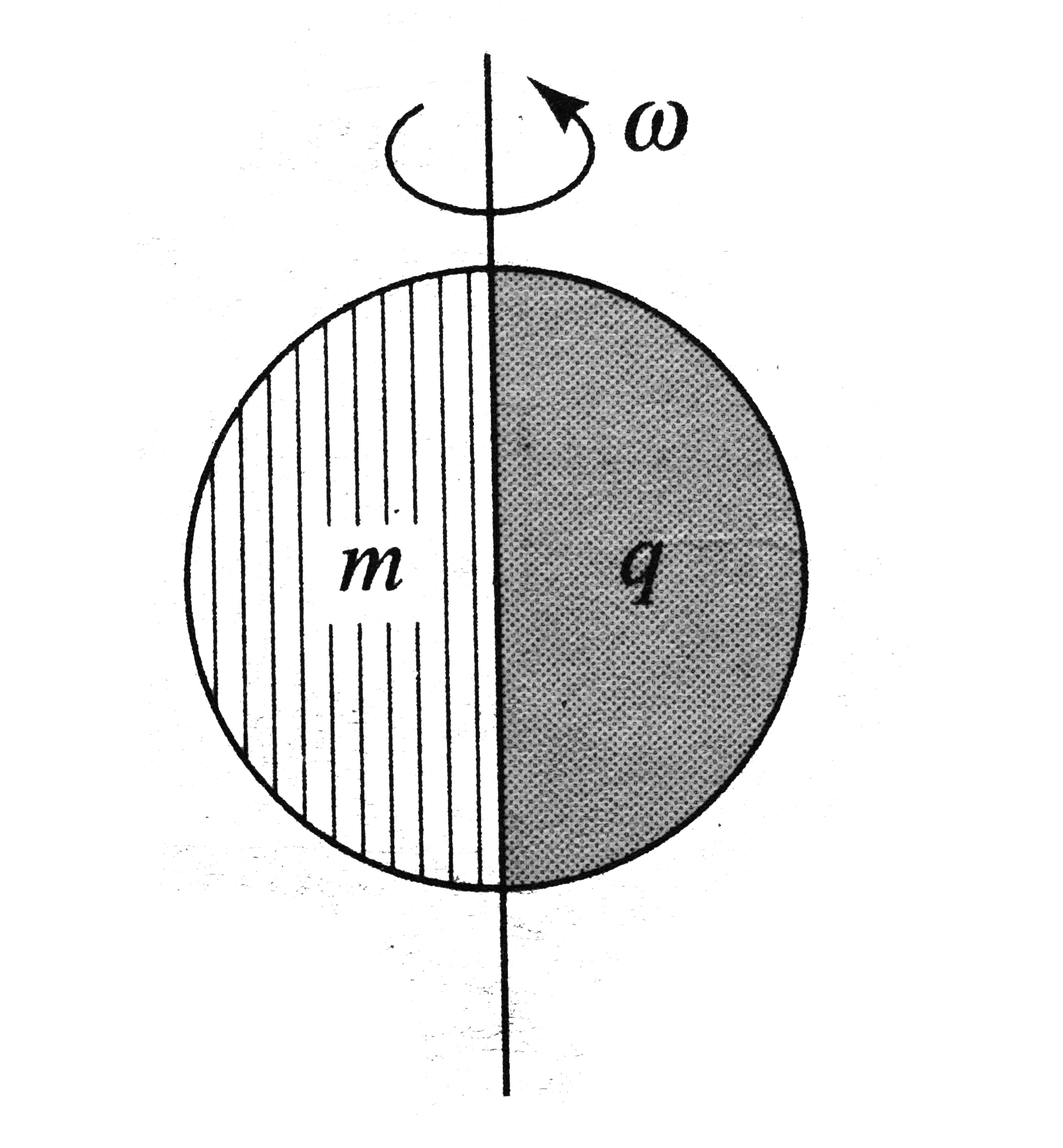View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.
View SolutionA ring of mass m and radius R is given a charge q. It is then rotated about its axis with angular velocity ω.Find
(ii) Magnetic field produced at the centre of ring.
View Solution