Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time.
Step by step video & image solution for Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and the inductor is constant in time. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - PROBLEMS28videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE - IA15videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - ALTERNATING CURRENTEXERCISE - Problem (Level - II)9videos
ALTERNATING CURRENT
- BOOK - AAKASH SERIESCHAPTER - APPENDICES ( REVISION EXERCISE )EXERCISE - REVISION EXERCISE (MAGNETISM AND MATTER )52videos
APPENDICES ( REVISION EXERCISE )
Similar Questions
Show that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View SolutionThe energy stored in the capacitor in the steady state is
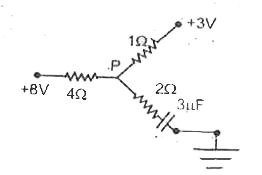View SolutionThe energy stored in 4μF capacitors is
View SolutionFind total energy stored in capacitors given in the circuit
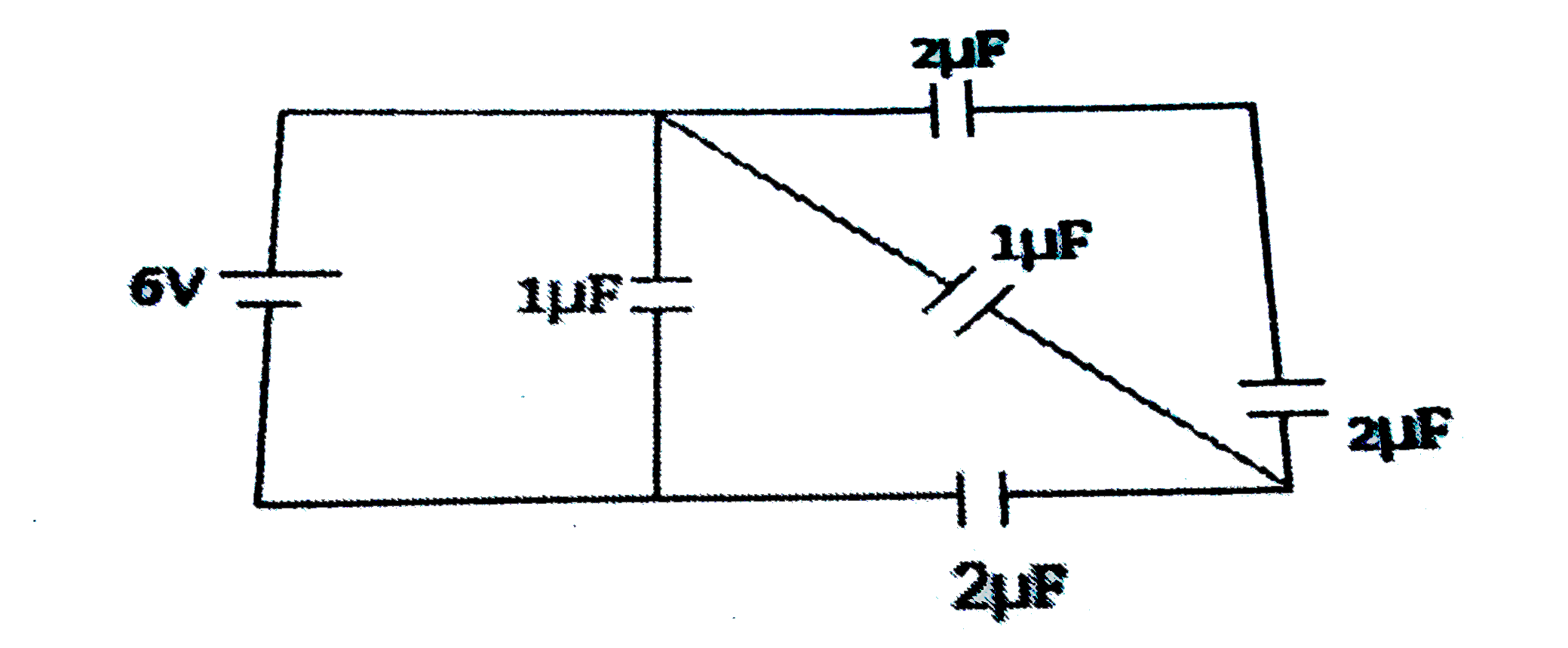View SolutionIn the circuit as shown in figure, energy stored in capacitor at steady state is
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
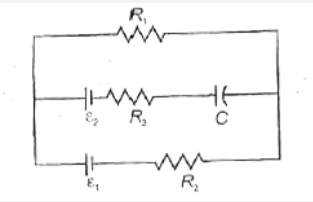View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View SolutionSwitch S is cloesd in the circuit at time t=0. Find the current through the capacitor and the inductor at any time t
View SolutionIn the given at t=0, switch S is closed.
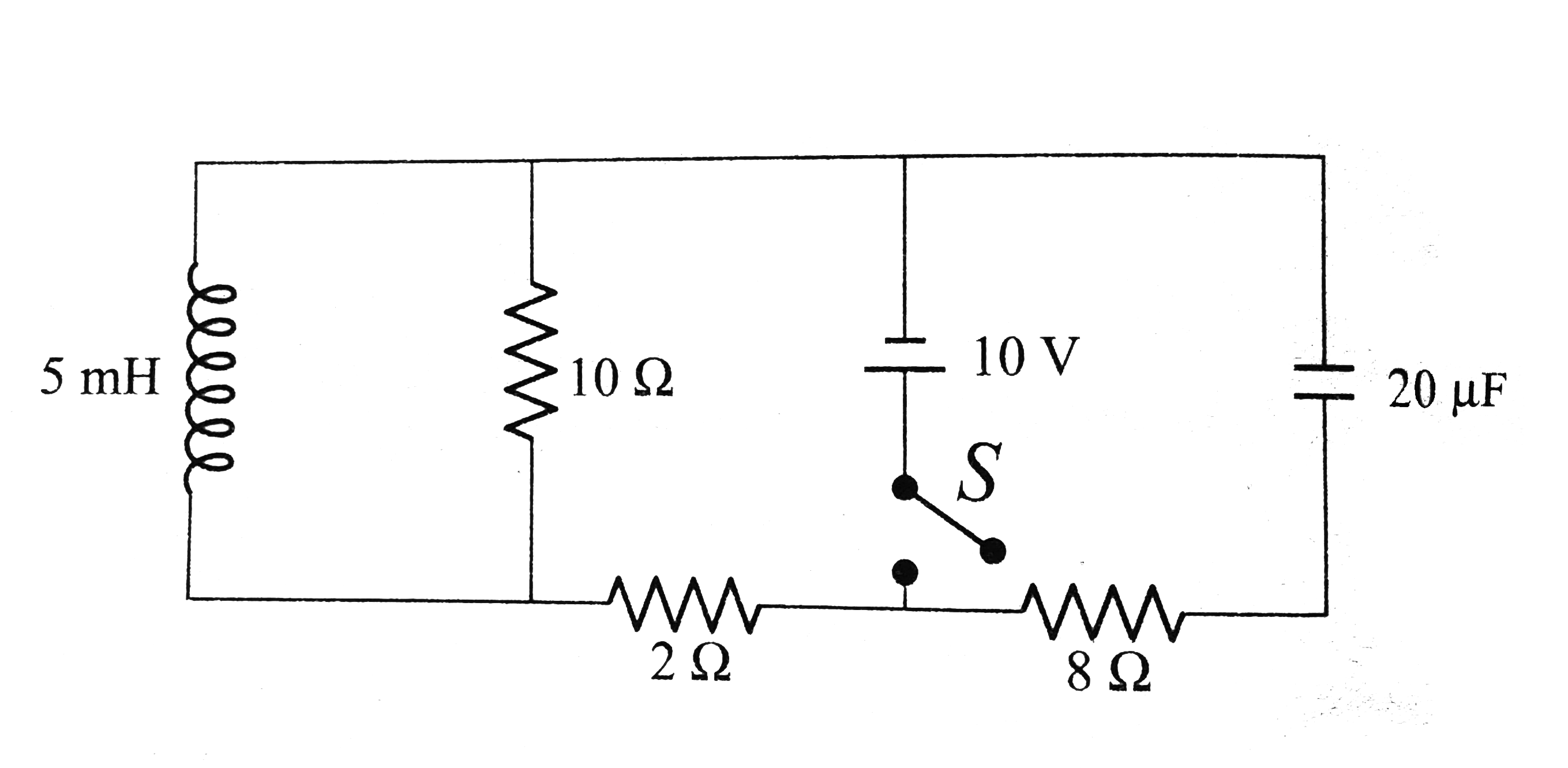
The energy stored in the capacitor and inductor, respectively, at t→∞ will beView SolutionA charge Q is given to the plates of an isolated capacitor of capacitance C. Now, the terminals of this capacitor are connected to the terminals of an inductor L at t = 0. After how much time will the energy stored in the capacitor and the Inductor become equal?
View Solution
