Derive expressions for the equivalent emf of series combination of electric cell.
To derive the expression for the equivalent electromotive force (emf) of a series combination of electric cells, we will follow these steps:
Step 1: Understand the Series Combination of Cells
In a series combination, the positive terminal of one cell is connected to the negative terminal of the next cell. This means that the same current flows through each cell.
Step 2: Define the Cells and Their Parameters
Let’s consider two cells in series:
- Cell 1 has an emf ϵ1 and an internal resistance R1.
- Cell 2 has an emf ϵ2 and an internal resistance R2.
Step 3: Calculate the Potential Differences
The potential difference across each cell can be expressed as:
- For Cell 1: VAB=ϵ1−IR1
- For Cell 2: VBC=ϵ2−IR2
Where I is the current flowing through the circuit.
Step 4: Total Potential Difference
The total potential difference (or the equivalent emf, ϵeq) across the combination of the two cells is the sum of the individual potential differences:
VAC=VAB+VBC
Substituting the expressions from Step 3:
VAC=(ϵ1−IR1)+(ϵ2−IR2)
Step 5: Simplify the Expression
Combining the terms gives:
VAC=ϵ1+ϵ2−I(R1+R2)
This shows that the equivalent emf ϵeq is:
ϵeq=ϵ1+ϵ2−I(R1+R2)
Step 6: Generalize for n Cells
For n cells in series, the equivalent emf can be generalized as:
ϵeq=ϵ1+ϵ2+ϵ3+...+ϵn
And the equivalent internal resistance is:
Req=R1+R2+R3+...+Rn
Conclusion
Thus, the equivalent emf of n cells in series is given by:
ϵeq=n∑i=1ϵi
And the equivalent internal resistance is:
Req=n∑i=1Ri
In a series combination, the positive terminal of one cell is connected to the negative terminal of the next cell. This means that the same current flows through each cell.
Let’s consider two cells in series:
- Cell 1 has an emf ϵ1 and an internal resistance R1.
- Cell 2 has an emf ϵ2 and an internal resistance R2.
The potential difference across each cell can be expressed as:
- For Cell 1: VAB=ϵ1−IR1
- For Cell 2: VBC=ϵ2−IR2
The total potential difference (or the equivalent emf, ϵeq) across the combination of the two cells is the sum of the individual potential differences:
VAC=VAB+VBC
Substituting the expressions from Step 3:
VAC=(ϵ1−IR1)+(ϵ2−IR2)
Combining the terms gives:
VAC=ϵ1+ϵ2−I(R1+R2)
This shows that the equivalent emf ϵeq is:
ϵeq=ϵ1+ϵ2−I(R1+R2)
For n cells in series, the equivalent emf can be generalized as:
ϵeq=ϵ1+ϵ2+ϵ3+...+ϵn
And the equivalent internal resistance is:
Req=R1+R2+R3+...+Rn
Thus, the equivalent emf of n cells in series is given by:
ϵeq=n∑i=1ϵi
And the equivalent internal resistance is:
Req=n∑i=1Ri
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)12videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE (VERY ANSWER QUESTIONS)44videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)27videos
CURRENT ELECTRICITY
- BOOK - AAKASH SERIESCHAPTER - COMMUNICATION SYSTEMS EXERCISE - PRACTICE EXERCISE (TV Antenna)16videos
COMMUNICATION SYSTEMS
- BOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA2videos
CURRENT ELECTRICITY
Similar Questions
(c) Derive the expression for the affective capacitance of a series combination of n capacitors.
View Solution(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.View Solution
Knowledge Check
- Question 1 - Select One
In series combination of resistances :
Ap.d. is same across each resistanceBtotal resistance is reducedCcurrent is same in each resistanceDall above are true.
Two cells of emf E1 and E2 have internal resistance r1 and r2. Deduce an expression for equivalent emf of their parallel combination.
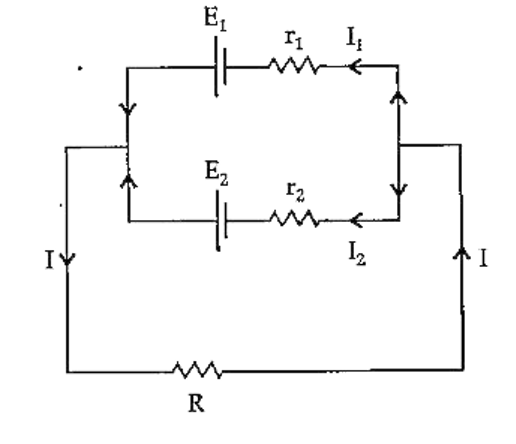 View Solution
View SolutionTwo cells of emfs ε1andε2 and internal resistances r1andr2 respectively are connected in parallel . Obtain expressions for the equivalent (i) resistance and , (ii) emf of the combination.
View SolutionDerive an expressions for torque in Certesian - Coordinates.
View SolutionThe equivalent resistance of the combination across AB is .
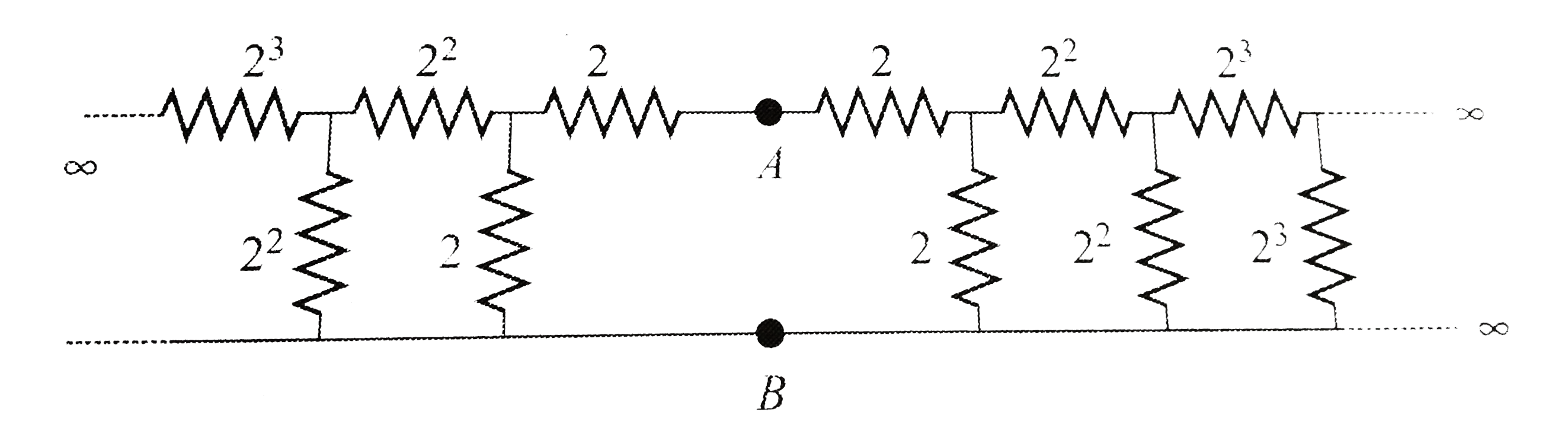 View Solution
View SolutionDerive an expression for the rotational kinetic energy.
View SolutionWrite the expression for equivalent spring constant of
(i) parallel combination of n−springs
(ii) series combination of n−springsView SolutionDerive an expression for the period of a geostationary satellite.
View Solution

