Write the expression for equivalent spring constant of
(i) parallel combination of n−springs
(ii) series combination of n−springs
The correct Answer is:(a) (i) (##RESWFPMPHYXIC04E01023_A01##)
Let extension in each spring is x then F1=K1x1
F2=K2x1,F3=K3x=……=Knx
F1+F2+F3+…..+Fn=F
⇒K1x+K2x+K3x+......+Knx=Keqx
⇒Keq=K1+K2+K3+....+Kn
(ii)(##RESWFPMPHYXIC04E01023_A02##)
Let F be the force in each spring and x1,x2,x3......xn
are the extensions in different springs
then F=K1x1=K2x2=K3x3=.......=Knxn
x1+x2+x3....+xn=x
⇒FK1+FK1+FK3+.......+FKn=FKeq
⇒FKeq=FK1+FK2+FK3+.........+FKn
To find the expressions for the equivalent spring constant for both the parallel and series combinations of n springs, we can break down the solution into two parts.
Part (i): Parallel Combination of n Springs
1. Understanding the Setup:
- When springs are arranged in parallel, they all share the same displacement when a force is applied.
- Let's denote the spring constant of each individual spring as k.
2. Calculating the Equivalent Spring Constant:
- In a parallel combination, the total force exerted by the springs is the sum of the forces exerted by each spring.
- According to Hooke's Law, the force exerted by a spring is given by F=k⋅x, where x is the displacement.
- If there are n springs, the total force can be expressed as:
Ftotal=n⋅(k⋅x)=n⋅k⋅x
- Therefore, the equivalent spring constant keq for the parallel combination is:
keq=n⋅k
Part (ii): Series Combination of n Springs
1. Understanding the Setup:
- In a series arrangement, the springs are connected end-to-end, and the same force acts on each spring.
- Again, let the spring constant of each spring be k.
2. Calculating the Equivalent Spring Constant:
- For springs in series, the total extension x is the sum of the extensions of each spring:
xtotal=x1+x2+x3+…+xn
- According to Hooke's Law, the extension of each spring can be expressed as:
xi=Fk
- Thus, the total extension becomes:
xtotal=Fk+Fk+…+Fk=n⋅Fk
- Rearranging gives:
xtotal=nFk
- The equivalent spring constant keq can be defined as:
F=keq⋅xtotal
- Substituting for xtotal:
F=keq⋅nFk
- Dividing both sides by F (assuming F≠0):
1=keq⋅nk
- Rearranging gives:
keq=kn
Final Expressions:
- For the parallel combination of n springs:
keq (parallel)=n⋅k
- For the series combination of n springs:
keq (series)=kn
- When springs are arranged in parallel, they all share the same displacement when a force is applied.
- Let's denote the spring constant of each individual spring as k.
- In a parallel combination, the total force exerted by the springs is the sum of the forces exerted by each spring.
- According to Hooke's Law, the force exerted by a spring is given by F=k⋅x, where x is the displacement.
- If there are n springs, the total force can be expressed as:
Ftotal=n⋅(k⋅x)=n⋅k⋅x
- Therefore, the equivalent spring constant keq for the parallel combination is:
keq=n⋅k
- In a series arrangement, the springs are connected end-to-end, and the same force acts on each spring.
- Again, let the spring constant of each spring be k.
- For springs in series, the total extension x is the sum of the extensions of each spring:
xtotal=x1+x2+x3+…+xn
- According to Hooke's Law, the extension of each spring can be expressed as:
xi=Fk
- Thus, the total extension becomes:
xtotal=Fk+Fk+…+Fk=n⋅Fk
- Rearranging gives:
xtotal=nFk
- The equivalent spring constant keq can be defined as:
F=keq⋅xtotal
- Substituting for xtotal:
F=keq⋅nFk
- Dividing both sides by F (assuming F≠0):
1=keq⋅nk
- Rearranging gives:
keq=kn
- For the parallel combination of n springs:
keq (parallel)=n⋅k
- For the series combination of n springs:
keq (series)=kn
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I
25 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II
36 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Solved Miscellaneous Problems
9 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
Knowledge Check
What is the mechanical equivalent of spring constant k in LC oscillating circuit?
A1LB1CCLCD1LC
(c) Derive the expression for the affective capacitance of a series combination of n capacitors.
View SolutionThe electrical analog of a spring constant k is
View SolutionDefine spring constant or force constant.
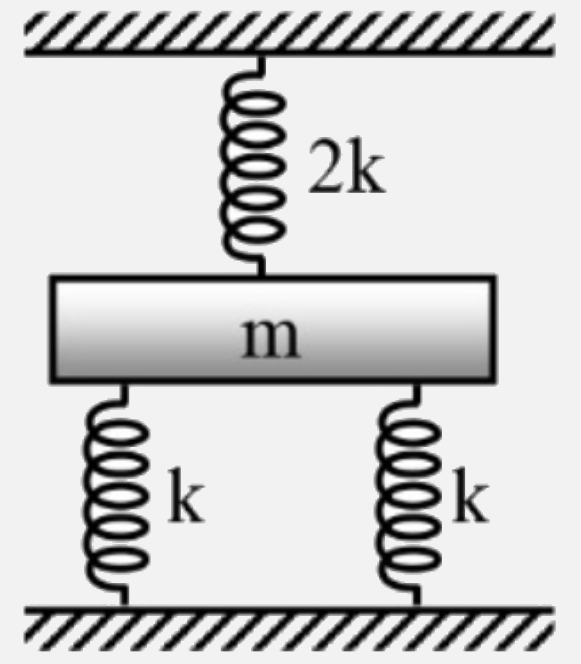
View SolutionIf ks and kp respectively are effective spring constant in series and parallel combination of springs as shown in figure, find kskp.

View SolutionWrite down the expression for the period of oscillation of a mass attached to (i) a horizontal spring and (ii) a vertical spring.
View SolutionPotential energy of an ideal spring, when stretched by 1 cm is U. Spring is now cut in two equal parts and connected in parallel. If the new combination of spring is compressed by 2 cm, then potential energy stored is
View SolutionExplain the meaning of force-constant of a spring.
View Solution