Masses 1 kg, 1.5 kg, 2 kg and M kg are situated at (2, 1, 1) (1, 2, 1) (2, -2, 1) and (-1, 4, 3). If the their centre of mass is situated at (1, 1, 3/2), the value of M is
1kg
2kg
1.5kg
3kg
The correct Answer is:C
To solve the problem, we need to find the mass M given the coordinates of four masses and the center of mass (COM). The masses and their coordinates are as follows:
- Mass m1=1kg at (2,1,1)
- Mass m2=1.5kg at (1,2,1)
- Mass m3=2kg at (2,−2,1)
- Mass m4=Mkg at (−1,4,3)
The center of mass is given as (1,1,32).
Step 1: Write the formula for the center of mass
The coordinates of the center of mass are given by:
xCOM=m1x1+m2x2+m3x3+m4x4m1+m2+m3+m4
yCOM=m1y1+m2y2+m3y3+m4y4m1+m2+m3+m4
zCOM=m1z1+m2z2+m3z3+m4z4m1+m2+m3+m4
Step 2: Substitute the known values into the equations
Using the given values:
1. For xCOM:
1=1⋅2+1.5⋅1+2⋅2+M⋅(−1)1+1.5+2+M
2. For yCOM:
1=1⋅1+1.5⋅2+2⋅(−2)+M⋅41+1.5+2+M
3. For zCOM:
32=1⋅1+1.5⋅1+2⋅1+M⋅31+1.5+2+M
Step 3: Simplify each equation
1. For xCOM:
1=2+1.5+4−M4.5+M
1(4.5+M)=7.5−M
4.5+M=7.5−M
2M=3⟹M=32=1.5kg
2. For yCOM:
1=1+3−4+4M4.5+M
1(4.5+M)=0+4M
4.5+M=4M
3M=4.5⟹M=4.53=1.5kg
3. For zCOM:
32=1+1.5+2+3M4.5+M
32(4.5+M)=4.5+3M
6.75+32M=4.5+3M
2.25=32M−3M
2.25=−32M⟹M=1.5kg
Final Answer
Thus, the value of M is 1.5kg.
- Mass m2=1.5kg at (1,2,1)
- Mass m3=2kg at (2,−2,1)
- Mass m4=Mkg at (−1,4,3)
The coordinates of the center of mass are given by:
Using the given values:
1=1⋅2+1.5⋅1+2⋅2+M⋅(−1)1+1.5+2+M
1=1⋅1+1.5⋅2+2⋅(−2)+M⋅41+1.5+2+M
32=1⋅1+1.5⋅1+2⋅1+M⋅31+1.5+2+M
1. For xCOM:
1=2+1.5+4−M4.5+M
1(4.5+M)=7.5−M
4.5+M=7.5−M
2M=3⟹M=32=1.5kg
1=1+3−4+4M4.5+M
1(4.5+M)=0+4M
4.5+M=4M
3M=4.5⟹M=4.53=1.5kg
32=1+1.5+2+3M4.5+M
32(4.5+M)=4.5+3M
6.75+32M=4.5+3M
2.25=32M−3M
2.25=−32M⟹M=1.5kg
Thus, the value of M is 1.5kg.
Similar Questions
Two bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
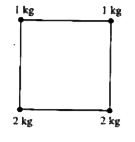 View Solution
View SolutionFour particles of mass 5,3,2,4kg are at the points (1,6),(−1,5),(2,−3),(−1,−4) . Find the coordinates of their centre of mass.
View SolutionFour point particles of masses 1.0 kg, 1.5 kg, 3.0 kg and 2.5 kg are placed at four corners of a rectangle of sides 4.0 cm and 3.0 cm as shown in the figure. The centre of mass of the system is at a point:
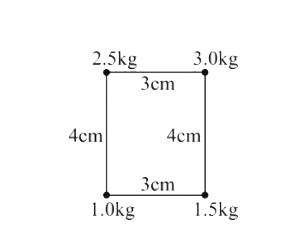 View Solution
View SolutionFour point particles of masses 1.0 kg, 1.5 kg, 3.0 kg and 2.5 kg are placed at four corners of a rectangle of sides 4.0 cm and 3.0 cm as shown in the figure. The centre of mass of the system is at a point:
 View Solution
View SolutionTwo bodies of mass 2 kg and 5 kg have position (1 m, 2 m, 1 m) and (3 m, 2 m, -1 m) respectively. The position vector of centre of mass is
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View SolutionThree point masses of 1kg, 2kg and 3kg lie at (0,0), (1,2), (3,−1) respectively. Calculate the coordinates of the centre of mass of the system.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles. Assume that D is situated at the origin.
View SolutionThree particles of masses 8 kg, 4 kg and 4 kg situated at (4,1), (-2,2) and (1,-3) are acted upon by external forces 6¯jN,−6¯iN and 14¯iN. The acceleration of centre of mass of the system is
View Solution

