A body of mass 4 kg is attached to another body of mass 2 kg with a massless rod. If the 4 kg mass is at (2i + 5j)m and 2 kg mass is at (4i + 2j)m, the centre of mass of the system is at (in m)
8i+12j
12(8i+12j)
13(8i+12j)
14(8i+12j)
The correct Answer is:C
To find the center of mass of the system consisting of two bodies, we can use the formula for the center of mass →Rcm:
→Rcm=m1→r1+m2→r2m1+m2
where:
- m1 and m2 are the masses of the two bodies,
- →r1 and →r2 are the position vectors of the two bodies.
Step 1: Identify the masses and their position vectors
Given:
- Mass m1=4kg at position →r1=2^i+5^jm
- Mass m2=2kg at position →r2=4^i+2^jm
Step 2: Substitute the values into the center of mass formula
Substituting the values into the center of mass formula:
→Rcm=4(2^i+5^j)+2(4^i+2^j)4+2
Step 3: Calculate the numerator
Calculating the terms in the numerator:
4(2^i+5^j)=8^i+20^j
2(4^i+2^j)=8^i+4^j
Adding these results together:
(8^i+20^j)+(8^i+4^j)=16^i+24^j
Step 4: Calculate the total mass
The total mass is:
m1+m2=4+2=6kg
Step 5: Divide the result by the total mass
Now, substituting back into the equation:
→Rcm=16^i+24^j6
Step 6: Simplify the result
This simplifies to:
→Rcm=166^i+246^j=83^i+4^j
Final Result
Thus, the center of mass of the system is at:
→Rcm=(83^i+4^j)m
---
- m1 and m2 are the masses of the two bodies,
- →r1 and →r2 are the position vectors of the two bodies.
Given:
- Mass m1=4kg at position →r1=2^i+5^jm
- Mass m2=2kg at position →r2=4^i+2^jm
Substituting the values into the center of mass formula:
Calculating the terms in the numerator:
2(4^i+2^j)=8^i+4^j
The total mass is:
Now, substituting back into the equation:
This simplifies to:
Thus, the center of mass of the system is at:
Similar Questions
A body A of mass 4 kg is dropped from a height of 100 m. Another body B of mass 2 kg is dropped from a height of 50 m at the same time. Then :
View SolutionA body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
View SolutionA body of mass 4kg moving with velocity 12m/s collides with another body of mass 6kg at rest. If two bodies stick together after collision , then the loss of kinetic energy of system is
View SolutionTwo bodies of masses 0.5 kg and 1 kg are lying in the X-Y plane at points (-1, 2) and (3, 4) respectively. Locate the centre of mass of the system.
View SolutionA rigid body consists of a 3kg mass connected to a 2kg mass by a massless rod. The 3kg mass is located at →r1=(2ˆi+5ˆj)m and the 2kg mass at →r2=(4ˆi+2ˆj)m. Find the length of rod and the coordinates of the centre of mass.
View SolutionA man of mass m=2kg is standing on a platform of mass M=5kg, then at any instant.
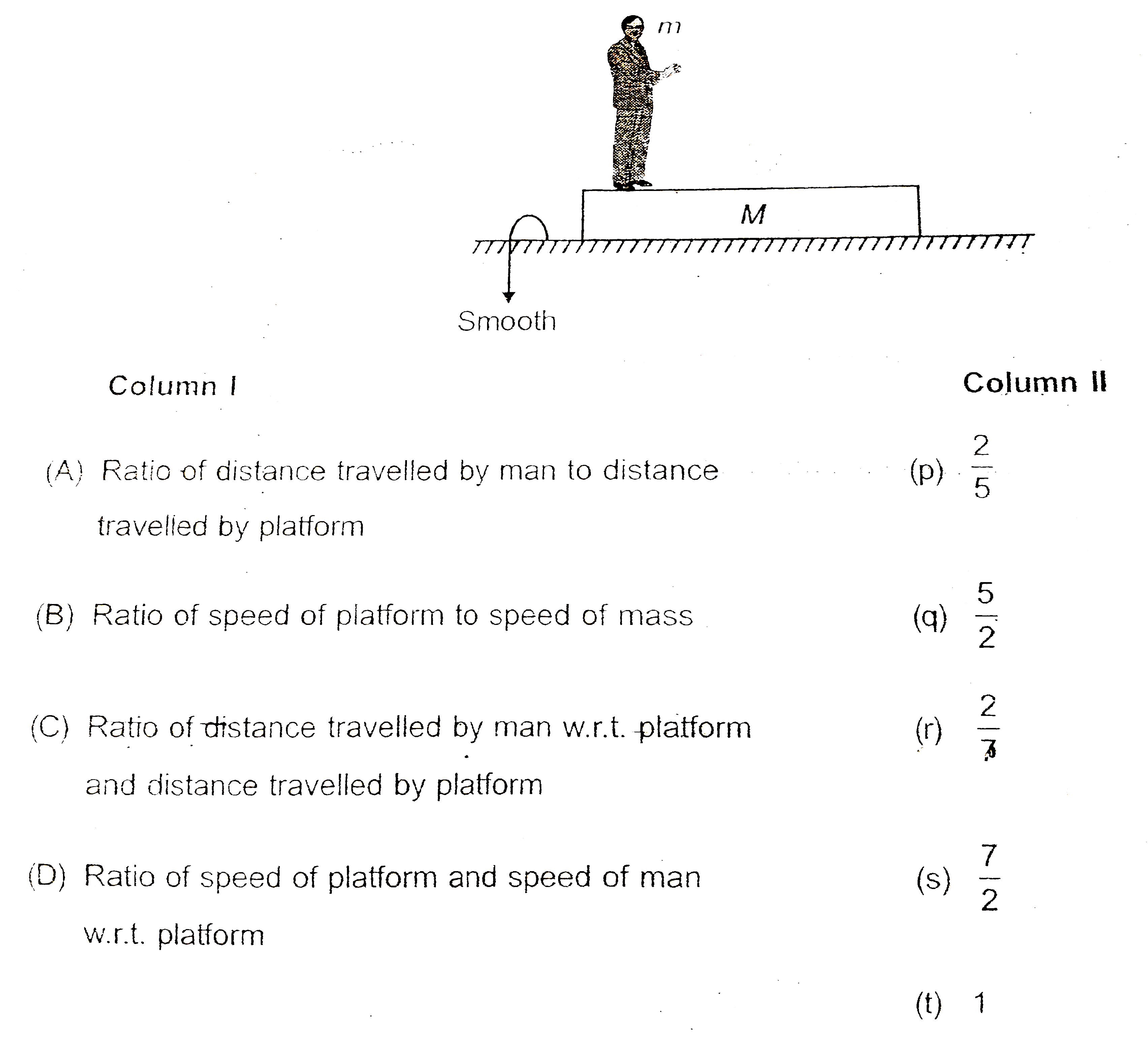 View Solution
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo particles of mass 5 kg and 10 kg respectively are attached to the twoends of a rigid rod of length 1 m with negligible mass. the centre of mass of the system from the 5 kg particle is nearly at a distance of :
View SolutionTwo bodies of mass 1kg and 3kg have position vectors ˆi+2ˆj+ˆk and −3ˆi−2ˆj+ˆk, respectively. The centre of mass of this system has a position vector.
View SolutionTwo bodies of mass 1kg and 3kg have position vectors ˆi+2ˆj+ˆk and −3ˆi−2ˆj+ˆk, respectively. The centre of mass of this system has a position vector.
View Solution

