There are three sections A,B and C in a class .Every section has some boy and some girl students in it .Probability of a girl being selected when one student is selected randomly from section A is 25 , that from section B is 49 and that from section C is 59.
If the number of girls in sections A is same as the number of boys in section C , then what is the ratio of number of boys in section A to the number of boys in section C ?
A)2:3
B)3:4
C)3:2
D)4:3
The correct Answer is:C
To solve the problem step by step, we will use the given probabilities to find the number of boys and girls in each section and then determine the required ratio.
Step 1: Understand the probabilities
The probability of selecting a girl from each section is given as follows:
- Section A: P(girl)=25
- Section B: P(girl)=49
- Section C: P(girl)=59
Step 2: Set up equations for the number of boys and girls
Let:
- GA = number of girls in section A
- BA = number of boys in section A
- GB = number of girls in section B
- BB = number of boys in section B
- GC = number of girls in section C
- BC = number of boys in section C
From the probabilities, we can express the number of girls and boys in each section:
1. For Section A:
GAGA+BA=25
This implies:
5GA=2(GA+BA)⟹5GA=2GA+2BA⟹3GA=2BA⟹BA=32GA
2. For Section B:
GBGB+BB=49
This implies:
9GB=4(GB+BB)⟹9GB=4GB+4BB⟹5GB=4BB⟹BB=54GB
3. For Section C:
GCGC+BC=59
This implies:
9GC=5(GC+BC)⟹9GC=5GC+5BC⟹4GC=5BC⟹BC=45GC
Step 3: Use the condition given in the problem
We know that the number of girls in section A is the same as the number of boys in section C:
GA=BC
Substituting BC from the equation we derived:
GA=45GC
Step 4: Express GC in terms of GA
From the equation GA=45GC:
GC=54GA
Step 5: Substitute GC back into the equation for BC
Now substituting GC into the equation for BC:
BC=45GC=45⋅54GA=GA
Step 6: Find the ratio of boys in section A to boys in section C
Now we have:
- From Section A: BA=32GA
- From Section C: BC=GA
Now we can find the ratio:
Ratio of BA to BC=BABC=32GAGA=32
Final Answer
Thus, the ratio of the number of boys in section A to the number of boys in section C is:
3:2
The probability of selecting a girl from each section is given as follows:
- Section A: P(girl)=25
- Section B: P(girl)=49
- Section C: P(girl)=59
Let:
- GA = number of girls in section A
- BA = number of boys in section A
- GB = number of girls in section B
- BB = number of boys in section B
- GC = number of girls in section C
- BC = number of boys in section C
1. For Section A:
GAGA+BA=25
This implies:
5GA=2(GA+BA)⟹5GA=2GA+2BA⟹3GA=2BA⟹BA=32GA
GBGB+BB=49
This implies:
9GB=4(GB+BB)⟹9GB=4GB+4BB⟹5GB=4BB⟹BB=54GB
GCGC+BC=59
This implies:
9GC=5(GC+BC)⟹9GC=5GC+5BC⟹4GC=5BC⟹BC=45GC
We know that the number of girls in section A is the same as the number of boys in section C:
GA=BC
Substituting BC from the equation we derived:
GA=45GC
From the equation GA=45GC:
GC=54GA
Now substituting GC into the equation for BC:
BC=45GC=45⋅54GA=GA
Now we have:
- From Section A: BA=32GA
- From Section C: BC=GA
Ratio of BA to BC=BABC=32GAGA=32
Thus, the ratio of the number of boys in section A to the number of boys in section C is:
3:2
Topper's Solved these Questions
- BOOK - ADDA247CHAPTER - PERMUTATION ,COMBINATION AND PROBABILITY EXERCISE - Previous Year Question25videos
PERMUTATION ,COMBINATION AND PROBABILITY
- BOOK - ADDA247CHAPTER - PERMUTATION ,COMBINATION AND PROBABILITY EXERCISE - Prelims Questions (Level - 2)35videos
PERMUTATION ,COMBINATION AND PROBABILITY
- BOOK - ADDA247CHAPTER - PERCENTAGEEXERCISE - PREVIOUS YEAR QUESTION26videos
PERCENTAGE
- BOOK - ADDA247CHAPTER - PROFIT AND LOSSEXERCISE - Previous Year Questions30videos
PROFIT AND LOSS
Similar Questions
The pie chart given below shows the number of students in 6 different sections. The total number of students is 1800.
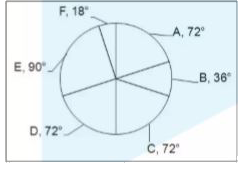
What is the ratio of number of students in section D to the number of students in section F and B?View SolutionIn a class of 60 students, the number of girls is one third the number of boys. Find the number of girls and boys in the class.
View Solution
Knowledge Check
- Question 1 - Select One
The total number of students in a class is 65. If the total number of girls in class 35, then the ratio of the total number of boys to the number of girls is:
Aa) 7:6Bb) 7:13Cc) 13:7Dd) 6:7 - Question 2 - Select One
In a school, the number of students in each section is equal to the number of sections. If the total number of students is 625, then find the numbr of sections
A10B20C15D25 - Question 3 - Select One
In a class, if 60% of the students are boys and the number of girls is 36, then the number of boys is:
A60B58C65D54
The number of boys and girls in a class are in the ratio 5:4. If the number of boys is 9 more than the number of girls, then number of boys is 9.
View SolutionIn class VI, there are 30 students. If the number of girls is 3 more than twice the number of boys, then the number of boys and girls are :
View SolutionThe pie chart given below shows the number of students in 6 different sections. The total number of students is 1800.
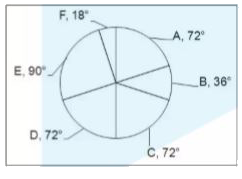
What is the difference between the number of students in section F to the number of students in section C?View SolutionThe number of boys and girls in a class are in the ratio 5:6 The number of boys is 5 less than the number of girls. What is the total number of students in that class.
View SolutionThe ratio of the number oif boys to that of girls in a school is 9:11. If the number of girls in the school is 2035, find:
a. number of boys is school.
b. number of students in school.View Solution

