In a stationary shop there are four types of colored sheets of red , blue ,green and white colors . The probability of selecting one red sheet out of the total sheets is 13 , the probability of selecting one blue sheet out of the sheets is 27 and the probability of selecting one white sheet out of the total sheets is 14 .the number of green sheets in the bag is 22.
If all the sheets are numbered as 1,2,3 ,...... and so on and one sheets is picked up at random ,then find the probability of picking up a sheet which is numbered as a multiple of 13 or 17.
A)18
B)17
C)58
D)910
The correct Answer is:A
To solve the problem step by step, we will first determine the total number of sheets in the stationary shop and then calculate the probability of picking a sheet that is numbered as a multiple of 13 or 17.
Step 1: Determine the total number of sheets (T)
We know the probabilities of selecting each colored sheet:
- Probability of red sheet (P(R)) = 1/3
- Probability of blue sheet (P(B)) = 2/7
- Probability of white sheet (P(W)) = 1/4
- Number of green sheets = 22
Using the formula for probability:
P(X)=Number of favorable outcomesTotal outcomes
We can express the probabilities in terms of the total number of sheets (T):
- For red sheets: RT=13 → R=T3
- For blue sheets: BT=27 → B=2T7
- For white sheets: WT=14 → W=T4
Step 2: Set up the equation
Since the total number of sheets is the sum of all colored sheets:
R+B+W+G=T
Substituting the values we have:
T3+2T7+T4+22=T
Step 3: Find a common denominator and solve for T
The least common multiple of 3, 7, and 4 is 84. We can rewrite the equation:
28T84+24T84+21T84+22=T
Combining the fractions:
73T84+22=T
Now, rearranging gives:
22=T−73T84
22=84T−73T84
22=11T84
Multiplying both sides by 84:
1848=11T
T=184811=168
Step 4: Calculate the number of sheets of each color
Now that we have T = 168, we can find the number of sheets of each color:
- Red sheets: R=1683=56
- Blue sheets: B=2×1687=48
- White sheets: W=1684=42
- Green sheets: G=22
Step 5: Find the number of favorable outcomes for multiples of 13 or 17
Next, we need to find how many sheets are numbered as multiples of 13 or 17.
Multiples of 13:
The multiples of 13 up to 168 are:
13,26,39,52,65,78,91,104,117,130,143,156
This gives us 12 multiples of 13.
Multiples of 17:
The multiples of 17 up to 168 are:
17,34,51,68,85,102,119,136,153
This gives us 9 multiples of 17.
Step 6: Calculate the total favorable outcomes
Now we add the favorable outcomes:
Total favorable outcomes = Multiples of 13 + Multiples of 17 = 12 + 9 = 21
Step 7: Calculate the probability
The probability of picking a sheet that is a multiple of 13 or 17 is given by:
P=Total favorable outcomesTotal outcomes=21168
Simplifying this:
P=18
Conclusion
Thus, the probability of picking a sheet which is numbered as a multiple of 13 or 17 is 18.
---
- Probability of red sheet (P(R)) = 1/3
- Probability of blue sheet (P(B)) = 2/7
- Probability of white sheet (P(W)) = 1/4
- Number of green sheets = 22
P(X)=Number of favorable outcomesTotal outcomes
- For red sheets: RT=13 → R=T3
- For blue sheets: BT=27 → B=2T7
- For white sheets: WT=14 → W=T4
R+B+W+G=T
Substituting the values we have:
T3+2T7+T4+22=T
28T84+24T84+21T84+22=T
Combining the fractions:
73T84+22=T
22=T−73T84
22=84T−73T84
22=11T84
1848=11T
T=184811=168
- Red sheets: R=1683=56
- Blue sheets: B=2×1687=48
- White sheets: W=1684=42
- Green sheets: G=22
The multiples of 13 up to 168 are:
13,26,39,52,65,78,91,104,117,130,143,156
This gives us 12 multiples of 13.
The multiples of 17 up to 168 are:
17,34,51,68,85,102,119,136,153
This gives us 9 multiples of 17.
Total favorable outcomes = Multiples of 13 + Multiples of 17 = 12 + 9 = 21
P=Total favorable outcomesTotal outcomes=21168
P=18
Topper's Solved these Questions
- BOOK - ADDA247CHAPTER - PERMUTATION ,COMBINATION AND PROBABILITY EXERCISE - Previous Year Question25videos
PERMUTATION ,COMBINATION AND PROBABILITY
- BOOK - ADDA247CHAPTER - PERMUTATION ,COMBINATION AND PROBABILITY EXERCISE - Prelims Questions (Level - 2)35videos
PERMUTATION ,COMBINATION AND PROBABILITY
- BOOK - ADDA247CHAPTER - PERCENTAGEEXERCISE - PREVIOUS YEAR QUESTION26videos
PERCENTAGE
- BOOK - ADDA247CHAPTER - PROFIT AND LOSSEXERCISE - Previous Year Questions30videos
PROFIT AND LOSS
Similar Questions
Knowledge Check
- Question 1 - Select One
The cost of 312 metre sheet is Rs.150, what will be the cost of 1 metre sheet ?
AApprox. Rs. 43BRs. 43CRs. 44DApprox. Rs. 43.50 - Question 2 - Select One
Figure shows a thin metallic triangular sheet ABC. The mass of the sheet is M. The moment of inertia of the sheet about side AC is :
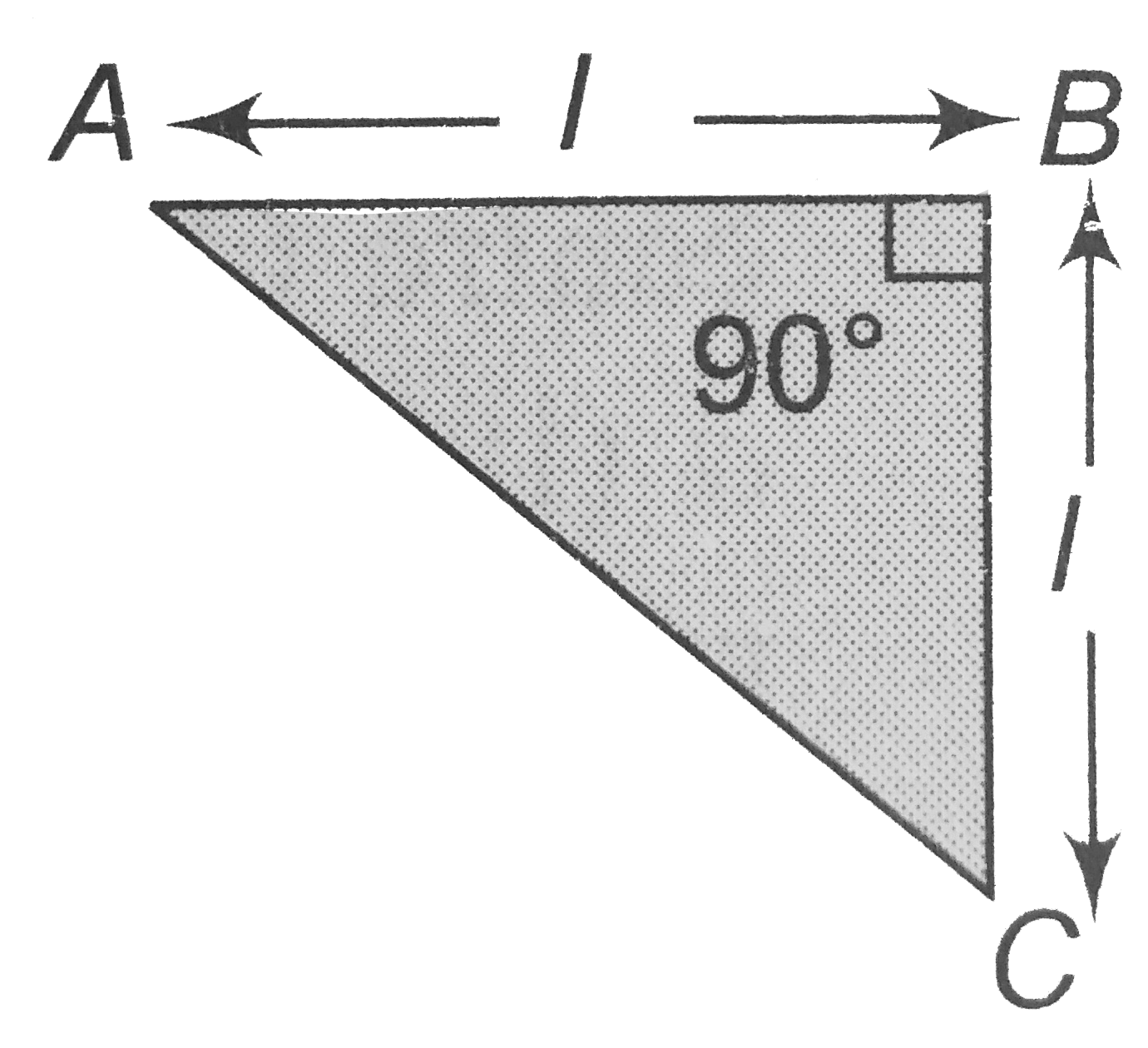 .AMl218BMl212CMl26DMl24
.AMl218BMl212CMl26DMl24 - Question 3 - Select One
Two sheets of thickness d and 3d, are touching each other. The temperature just outside the thinner sheet is T1 and on the side of the thicker sheet is T3. The interface temperature is T2.T1,T2andT3 are in arithmetic progression. The ratio of thermal conductivity of thinner sheet to thicker sheet is
A1:3B3:1C2:3D3:9
The area of a square sheet is 250 sq. cm. If one-fourth of the sheet is painted red, then half of the sheet is painted green and the remaining is painted white. Find the percentage of the area painted in white.
View SolutionDefects on plywood sheet occur at random with the average of one defect per 50 Sq. ft. Find the probability that such a sheet has no defect. Use e−1=0.3678.
View SolutionA square-sheet of paper ls four- folded (i.e. 4 layer of paper are made of the sheet). Then it is cut on one edge of the triangular fold . Find the figure pattern of sheet on unfolding from the answer figures.
 View Solution
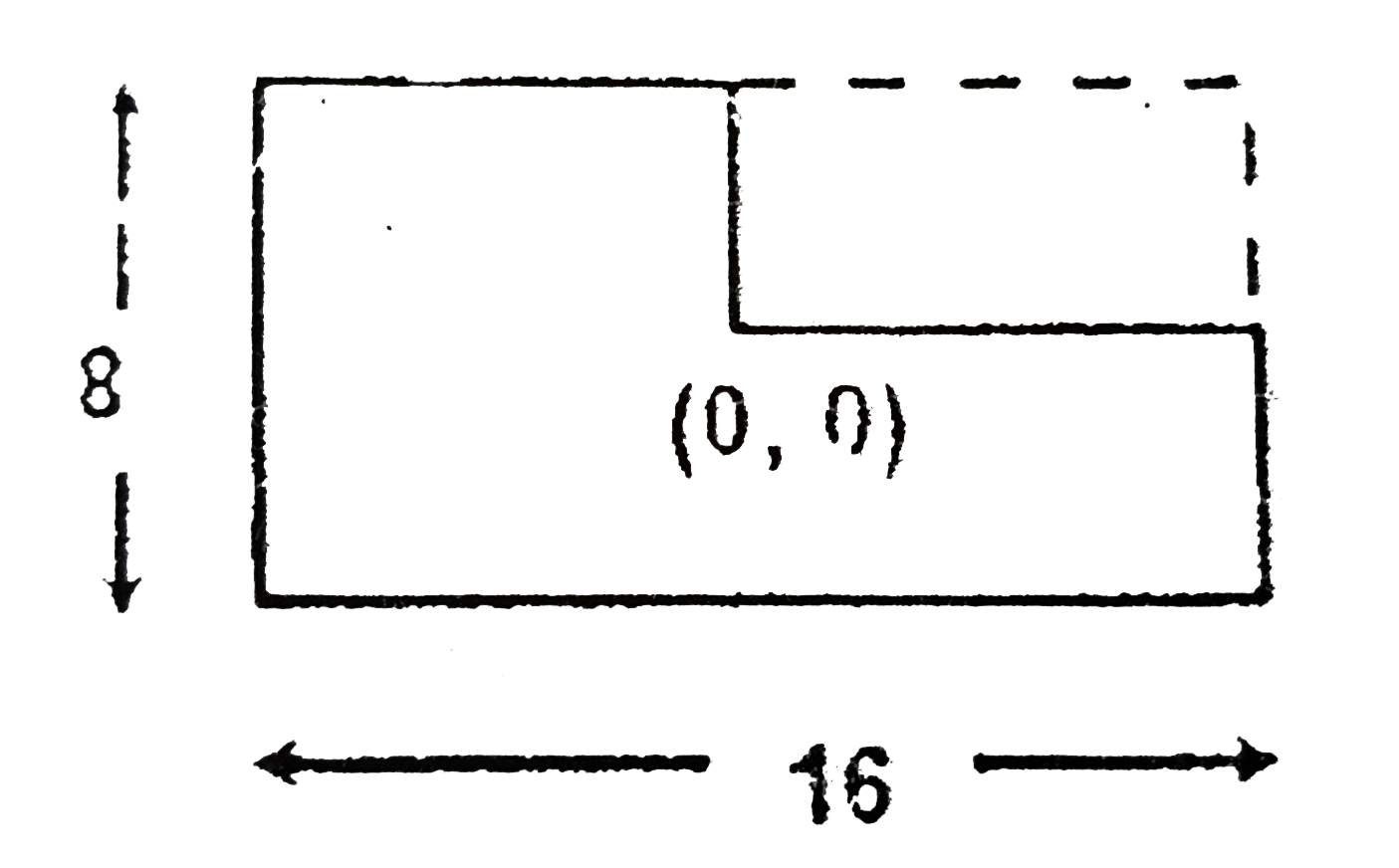
View SolutionFrom a 16cm×8cm rectangular uniform plane sheet, exactly one quarter of the sheet is removed as shown in figure. If the origin be taken at the centre of the sheet considered as shown in the figure the coordinates of the centre of mass of the remaining sheet is
 View Solution
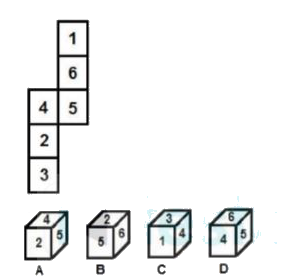
View SolutionSelect the dices that can be formed by folding the given sheet.
 View Solution
View Solution

