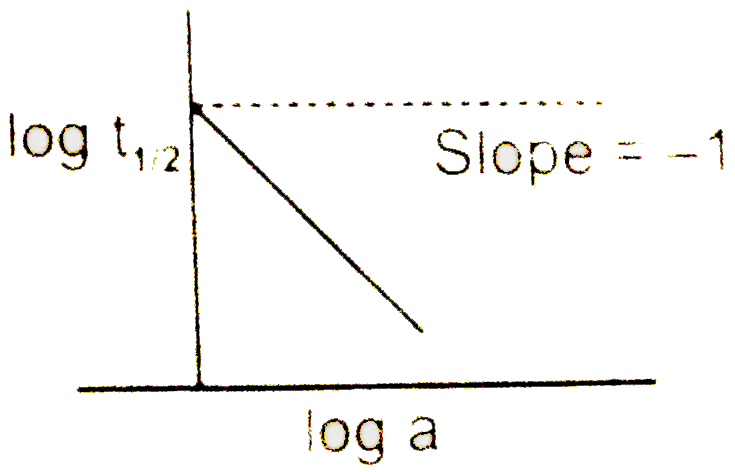
A graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
Solution in Telugu
−d[A]dt=K
−d[A]dt=K[A]
−d[A]dt=K[A]2
−d[A]dt=K[A]3
The correct Answer is:C
Step by step video & image solution for A graph between log t_((1)/(2)) and log a (abscissa), a being the initial concentration of A in the reaction For reaction AtoProduct, the rate law is : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)2videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)3videos
CHEMICAL KINETIC & NUCLEAR CHEMISTRY
- BOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level 3 - Assertion - Reason Type Questions1videos
SURFACE CHEMISTRY
Similar Questions
The reaction of A2 and B2 follows the equation
A2(g)+B2(g)→2AB(g)
The following data were observed
[A2]0[B2]0Initial rate of appearance of AB(g)(inMs−10.100.102.5×10−40.200.105×10−40.200.2010×10−4
The value of rate constatnt for the above reaction is :02:41View SolutionHalf-life (t1/2) and completion time (T) of the reaction (A→2B) are if initial concentration A is 1M and k = 0.001M/ min :
02:04View Solutioneach question constain STATEMENT-1(Assertion ) and STATEMENT - 2 (reason). examine the statement carefully and work the correct answer accoridng to the instructions given below :
STATEMENT-1: Dispersed phase particles of colloidal solution cannot pass through ultra -filter paper.
STATEMENT-2: The size of colloidal particles are larger than the size of true solution particles.01:32View SolutionFollowing is the graph between log T_(50) and log a ( a = initial concentration) for a given reaction at 27^(@)C . Hence order is
01:50View SolutionFollowing is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 27∘C.
Find the order of reaction.02:22View SolutionA graph between log t_((1)/(2)) and log a (abscissa), a being the initial concentration of A in the reaction For reaction Ato Product, the rate law is :
04:51View SolutionFollowing is the graph between log T_(50) and log a (a = initial concentration) for a given reaction at 27^(@)C . Hence, order is
01:32View SolutionFor a second order reaction, 2" A"to Products, a plot of log t_(1//2) vs log a (where a is the initial concentration) will give an intercept equal to which of the following ?
View SolutionThe graph between log t1/2 and log a at a given temperature is
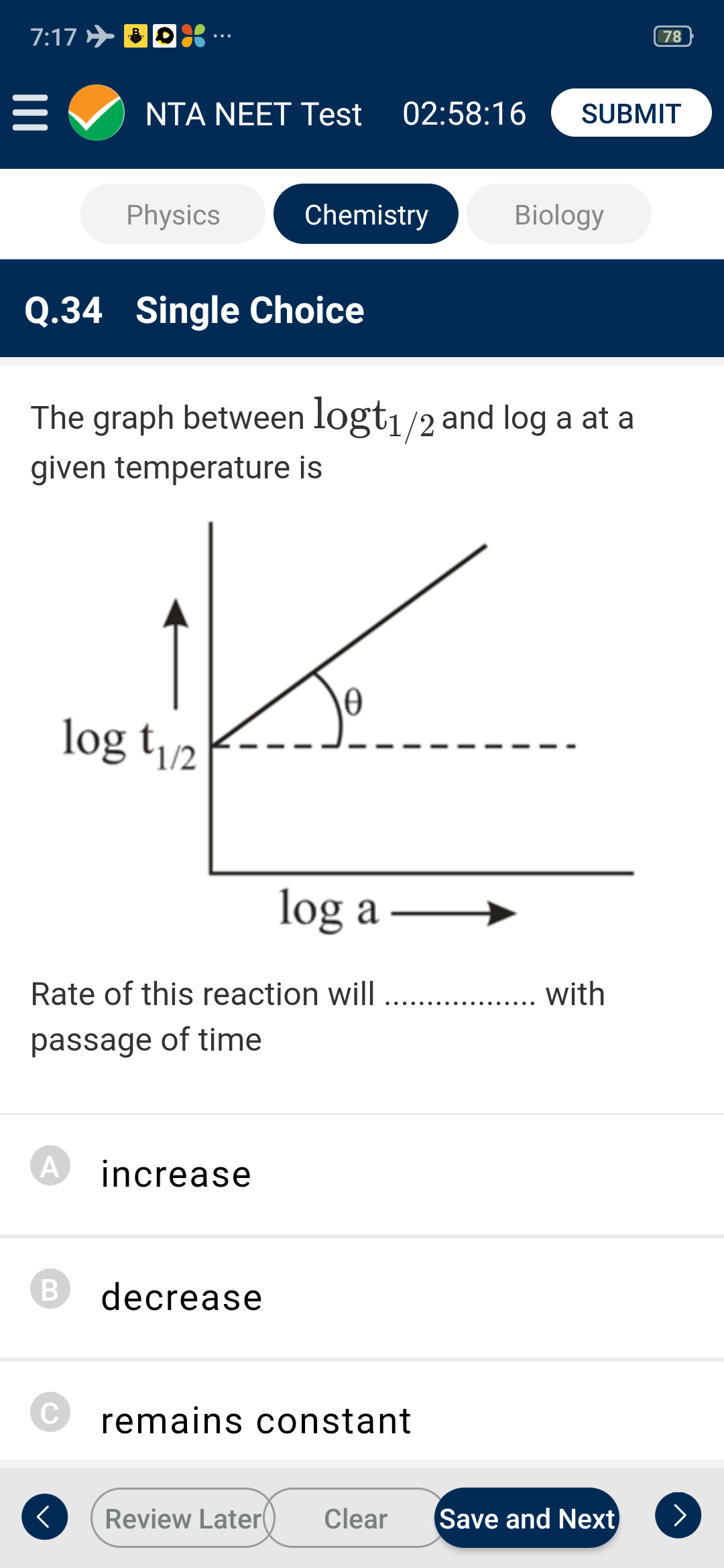
Rate of this reaction will …….with passage of time04:19View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
03:06View SolutionA graph between log t1/2 and log a (abscissa), a being the initial concentration of A in the reaction A → product, is depicted in the figure. The rate law is
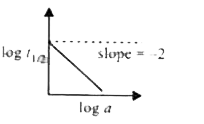02:18View Solution27∘C ताप पर दी गई अभिक्रिया के लिए logt1/2 तथा log a (a प्रारंभिक सान्द्रता) के मध्य ग्राफ निम्न है
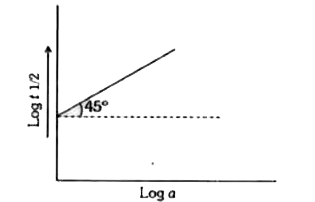02:58View SolutionA graph between log t_((1)/(2)) and log a (abscissa), a being the initial concentration of A in the reaction For reaction Ato Product, the rate law is :
03:39View SolutionFollowing is the graph between log T_(50) and log a ( a = initial concentration) for a given reaction at 27^(@)C . Hence order is
05:24View SolutionFollowing is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 300K
Find the order of reaction.03:01View SolutionWhat will be the order of reaction for a chemical change having following graph of log t12 versus log a?
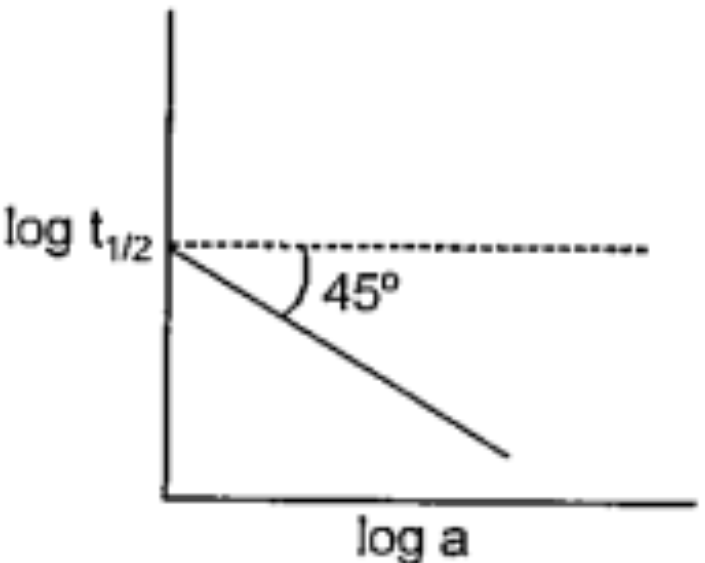(a = initial concentration of reaction: t12= half-life) 04:39View Solution