Explain reversible and irreversible processes. Describe the working of Carnot engine. Obtain an expression for the efficiency.

Text Solution

Verified by Experts

Reversible process : In reversible process a thermodynamic system can be retraced back in opposite direction to the changes that take place in the direct process or in forward process. Finally the system must be in thermal equilibrium with surroundings even after returning to original state with no other change any where else in the universe. A reversible process is only an ideal concept.
Conditions for reversible process: A reversible process must obey the following conditions.
(1) Changes must take place at an infinitesimally slow rate.
(2) The system must always be in thermal and mechanical equilibrium with surroundings.
(3) There should be no loss of energy in any form.
(4) No amount of heat is to be converted into electric or magnetic forms.
Examples for reversible process : (1) Peltier effect and Seebeck effect.
(2) Fusion of ice and vapourisation of water.
Irreversible process: A thermodynamic process that cannot be taken back in opposite direction is called an irreversible process. Examples:
(1) Work done against friction.
(2) Magnetization of materials. In an irreversible process the thermodynamic system cannot be operated in reverse direction without loss of energy or system cannot be taken to original state without loss of energy.
(3) All spontaneous natural processes are irreversible.
(4) Diffusion of gases.
(5) Joule heating in a conductor by passing current through it.
Carnot.s Engine : Carnot.s engine works on the principle of reversible process within the temperatures $T_{1} and T_{2}$ . It consists of four continuous processes. The total process is known as Carnot Cycle.
Step 1 : In Carnot cycle the 1st step consists of isothermal expansion of gases. So temperature T is constant, P, V changes are shown as $P_{1} V_{1} T_{1} to - - \to P_{2} V_{2} T_{1}$
Work done in isothermal process $W_{1 \to 2} = Q_{i} = μ R T_{1} {log}_{e} (\frac{V_{2}}{V_{1}})$ ........ (1)
Step 2: In this stage gases will expand adiabatically. So energy to the system Q is constant. So P, V relation is :

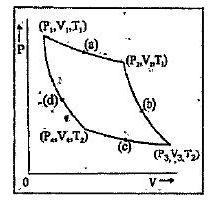
$P_{2} V_{2} T_{1} to - - \to P_{3} V_{3} T_{2}$
Work done in adiabatic process $W_{2 \to 3} = \frac{μ R (T_{1} - T_{2})}{γ - 1}$ ...(2)
Step 3 : In this stage gases will be compressed isothermally. So $P_{1} V$ changes are
$P_{3} V_{3} T_{2} to - - \to P_{4} V_{4} T_{2}$
Work done in isothermal compression
$W_{3 \to 4} = Q_{2} = μ R T_{2} {log}_{e} (\frac{V_{3}}{V_{4}})$ .....(3)
Step 4: In the fourth stage the gas suffers adiabatic compression and returns to original stage. So P. V changes are $P_{4} V_{4} T_{2} to - - \to P_{1} V_{1} T_{1}$
Work done $W_{4 \to 1} = μ R \frac{(T_{2} - T_{1})}{γ - 1}$ ..... (4)
Total work done in Carnot Cycle $W = W_{1, 2} + W_{2, 3} + W_{3, 4} + W_{4, 1}$
Total work done $W = μ R T_{1} log (\frac{V_{2}}{V_{1}}) + \frac{μ R}{γ - 1} (T_{1} - T_{2}) - μ R T_{2} log (\frac{V_{3}}{V_{4}}) - \frac{μ R}{γ - 1} (T_{1} - T_{2})$
$∴ W = μ R T_{1} log (\frac{V_{2}}{V_{1}}) - μ R T_{2} log (\frac{V_{3}}{V_{4}})$
The total work done $W + Q_{1} - Q_{2}$ i.e, the difference to heat energy absorbed from source and heat energy given to sink
Efficiency of Carnot engine : Efficiency of Carnot engine $η = \frac{work done by Carnot engine}{heat energy supplied}$
$∴ η = \frac{Q_{1} - Q_{2}}{Q_{1}} or η = 1 - \frac{Q_{2}}{Q_{1}} = 1 - \frac{T_{2}}{T_{1}}$

Updated on:21/07/2023

The efficiency of a Carnot heat engine
Ais independent of the temperature of the source and the sink
Bis independent of the working substance
Ccan be $10 %$
Din not affected by the thermal capacity of the source of the sink
Efficiency of Carnot engine is $100 %$ if
A $T_{2} = 273 K$
B $T_{2} = 0 K$
C $T_{1} = 273 K$
D $T_{1} = 0 K$
The efficiency of carnot engine depends on
Atemperature of sink only
Btemperature of source and sink
Cvolume of cylinder of engine
Dtemperature of source