In Fig.4.73, ABC is a triangle with ∠B=90∘,BC=3cmandAB=4cm. D is point on AC such that AD = 1 cm and E is the midpoint of AB. Join D and E and extend DE to meet CB at F. Find BF.
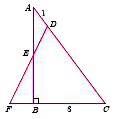
The correct Answer is:1
Topper's Solved these Questions
- GEOMETRYBOOK - NCERT TAMILCHAPTER - GEOMETRYEXERCISE - EXERCISE 4.1
8 Videos
- GEOMETRYBOOK - NCERT TAMILCHAPTER - GEOMETRYEXERCISE - EXERCISE 4.2
8 Videos
- COORDINATE GEOMETRY BOOK - NCERT TAMILCHAPTER - COORDINATE GEOMETRY EXERCISE - TRY THIS
15 Videos
- MENSURATIONBOOK - NCERT TAMILCHAPTER - MENSURATIONEXERCISE - Unit Exercise - 7
10 Videos
Similar Questions
In figure, ABC is a triangle with ∠B=90∘, BC = 3cm and AB = 4cm. D is a point on AC such that AD = 1cm and E is the mid- point of AB. Join D and E and extend DE to meet CB extended at F. Then BF is equal to
View SolutionIn a ΔABC,AB=AC=17cmD is a point on BC such that AD=15,CD=4cm, find BD=?
View Solution
Knowledge Check
The area of ΔABC is 44 cm2 . If D is the midpoint of BC and E is the midpoint of AB, then the area ( in cm2) of ΔBDE is :
A5.5B22C11D44In ΔABC,∠C=90∘ And D is a point on CB such that AD is the bisector of ∠A . If AC = 5cm and BC = 12 cm, then what is the length of AD ?
A103cmB203cmC53√13cmD56√13cmFor a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
Aa) 5 cmBb) 4 cmCc) 3 cmDd) 6 cm
ABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
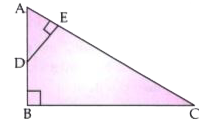
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionIn triangle ABC, D is a point in side AB such that AB = 4AD and E is a point in AC such that AC = 4AE. Show that BC : DE = 4:1
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC . Prove that DE=14BC .
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionFor a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
View Solution
