In triangle ABC, D is a point in side AB such that AB = 4AD and E is a point in AC such that AC = 4AE. Show that BC : DE = 4:1
To solve the problem, we need to show that the ratio BC:DE=4:1 in triangle ABC given the conditions about points D and E. Here is a step-by-step solution:
Step 1: Understand the given information
We have triangle ABC with points D on side AB and E on side AC such that:
- AB=4AD
- AC=4AE
Step 2: Define the segments
Let:
- AD=x
- Then, AB=4AD=4x
- Therefore, DB=AB−AD=4x−x=3x
Similarly, for point E:
- AE=y
- Then, AC=4AE=4y
- Therefore, EC=AC−AE=4y−y=3y
Step 3: Construct midpoints
Let P be the midpoint of AB and Q be the midpoint of AC.
- Thus, AP=PB=AB2=4x2=2x
- And AQ=QC=AC2=4y2=2y
Step 4: Apply the Midpoint Theorem
According to the Midpoint Theorem:
- The line segment PQ is parallel to BC and PQ=12BC.
Step 5: Analyze triangle APQ
In triangle APQ:
- Since D is on AB such that AD=x, we can conclude that D divides AP in the ratio 1:3 (since AD:DB=1:3).
- Similarly, since E is on AC such that AE=y, E divides AQ in the ratio 1:3.
Step 6: Apply the Midpoint Theorem again
Since D and E are midpoints of segments AP and AQ respectively, we can say:
- DE is parallel to PQ and DE=12PQ.
Step 7: Relate DE and BC
From the previous steps, we have:
- PQ=12BC
- Therefore, DE=12PQ=12(12BC)=14BC
Step 8: Establish the ratio
Now we can establish the ratio:
BC:DE=BC:(14BC)=4:1
Conclusion
Thus, we have shown that BC:DE=4:1.
We have triangle ABC with points D on side AB and E on side AC such that:
- AB=4AD
- AC=4AE
Let:
- AD=x
- Then, AB=4AD=4x
- Therefore, DB=AB−AD=4x−x=3x
- AE=y
- Then, AC=4AE=4y
- Therefore, EC=AC−AE=4y−y=3y
Let P be the midpoint of AB and Q be the midpoint of AC.
- Thus, AP=PB=AB2=4x2=2x
- And AQ=QC=AC2=4y2=2y
According to the Midpoint Theorem:
- The line segment PQ is parallel to BC and PQ=12BC.
In triangle APQ:
- Since D is on AB such that AD=x, we can conclude that D divides AP in the ratio 1:3 (since AD:DB=1:3).
- Similarly, since E is on AC such that AE=y, E divides AQ in the ratio 1:3.
Since D and E are midpoints of segments AP and AQ respectively, we can say:
- DE is parallel to PQ and DE=12PQ.
From the previous steps, we have:
- PQ=12BC
- Therefore, DE=12PQ=12(12BC)=14BC
Now we can establish the ratio:
BC:DE=BC:(14BC)=4:1
Thus, we have shown that BC:DE=4:1.
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:PYTHAGORAS THEOREM
Explore 5 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:RECTILINEAR FIGURES
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:INEQUALITIES
Explore 7 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Graphical solution
Explore 10 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
Similar Questions
In triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionIn ΔABC,AB=ACandD is a point an side AC such that AD = BD = BC . Show that : ∠ADB=108∘
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
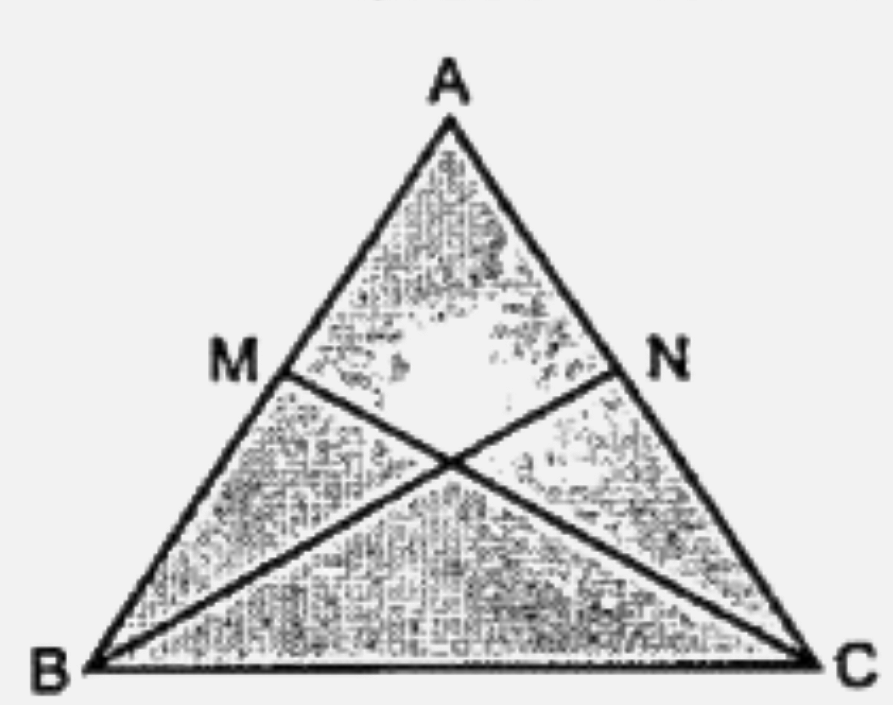
BN=CM
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionIn a scalene triangle ABC ,AD and BE are medians F is a point in AC so that DF//BE. Show that : AC = 4× EF.
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that

ΔBMC≅ΔCNB
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
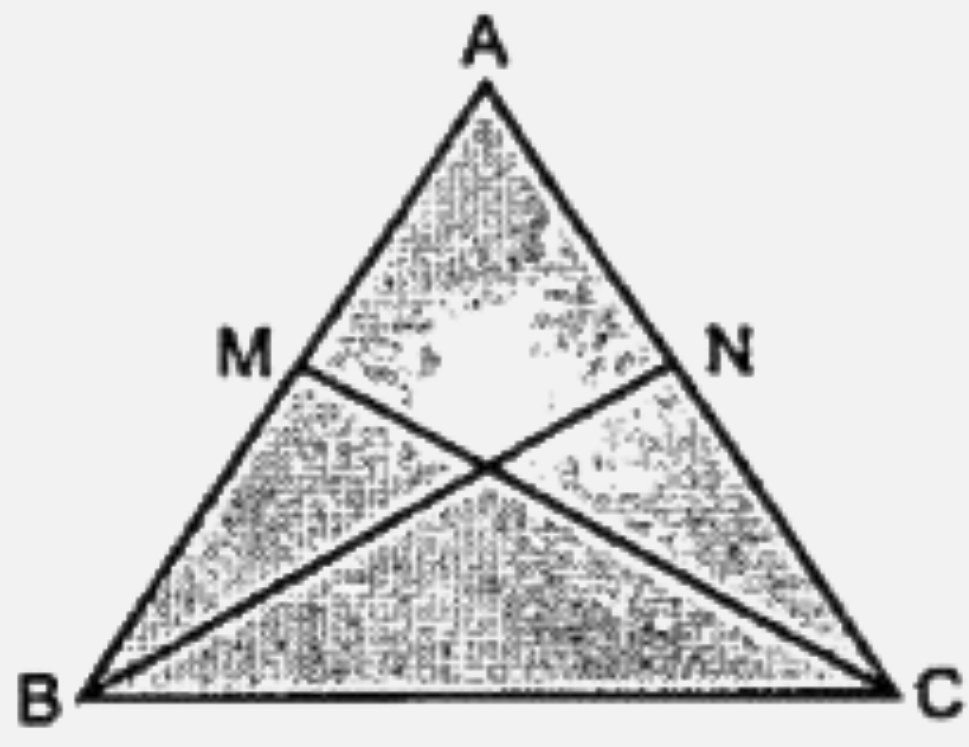
AM=AN
View SolutionABC is a triangle in which AB = AC and D is any point on BC. Prove that:
AB2−AD2=BD.CD
View Solution