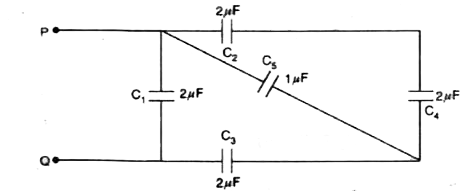
Find the equivalent capacitance between P and Q for the configuration shown below in the figure (a).
Text Solution
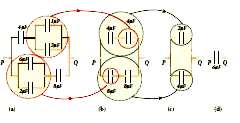
The capacitors 1μFand3μF are connected in parallel and 6μFand2μF are also separately connected in parallel. So these parallel combinations reduced to equivalent single capacitances in their respective positions, as shown in the figure (b).
Ceq=1μF+3μF=4μF
Ceq=6μF+2μF=8μF
From the figure (b), we infer that the two 4μF capacitors are connected in series and the two 8μF capacitors are connected in series. By using formula for the series, we can reduce to their equivalent capacitances as shown in figure (c).
1Ceq=14+14+14=12 ⇒Ceq=2μ F
and
1Ceq=18+18=14 ⇒Ceq=4μ F
From the figure (c), we infer that 2μFand4μF are connected in parallel. So the equivalent capacitance is given in the figure (d).
Ceq=2μF+4μF=6μF
Thus the combination of capacitances in figure (a) can be replaced by a single capacitance 6μF.
|
Topper's Solved these Questions
- ELECTROSTATICSBOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - EVALUATION (Multiple choice questions)
15 Videos
- ELECTROSTATICSBOOK - NCERT TAMILCHAPTER - ELECTROSTATICSEXERCISE - Exercises
23 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - NCERT TAMILCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ADDITIONAL EXERCISES
1 Videos
- MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - NCERT TAMILCHAPTER - MAGNETISM AND MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - EVALUATION (IV. Numerical problems)
10 Videos
Similar Questions
Knowledge Check
The equivalent capacitance between P and Q is.
 .A10μFB20μFC5μFD15μF
.A10μFB20μFC5μFD15μFFind the equivalent capacitance between P and Q in the circuit shown in the figure:
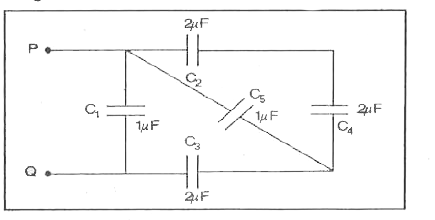 A2μFB4μFC6μFD3μF
A2μFB4μFC6μFD3μFThe equivalent capacitance between points P and Q of the combination shown in figure is
 ACB2CC32CDC2
ACB2CC32CDC2
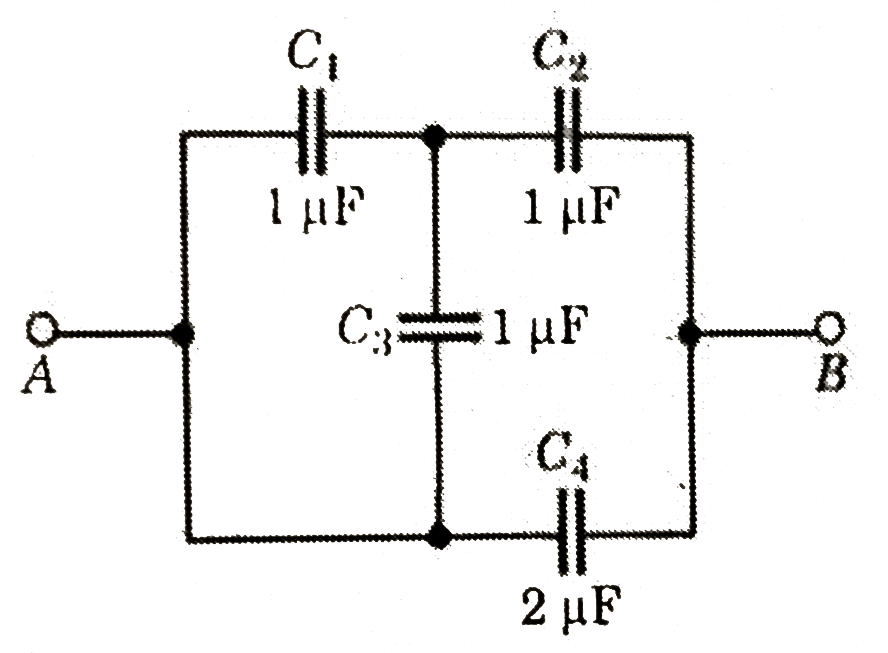
Find the equivalent capacitance between points A and B for the network shown in figure.
View SolutionFind equivalent capacitance between points A and B shown in figure

View Solution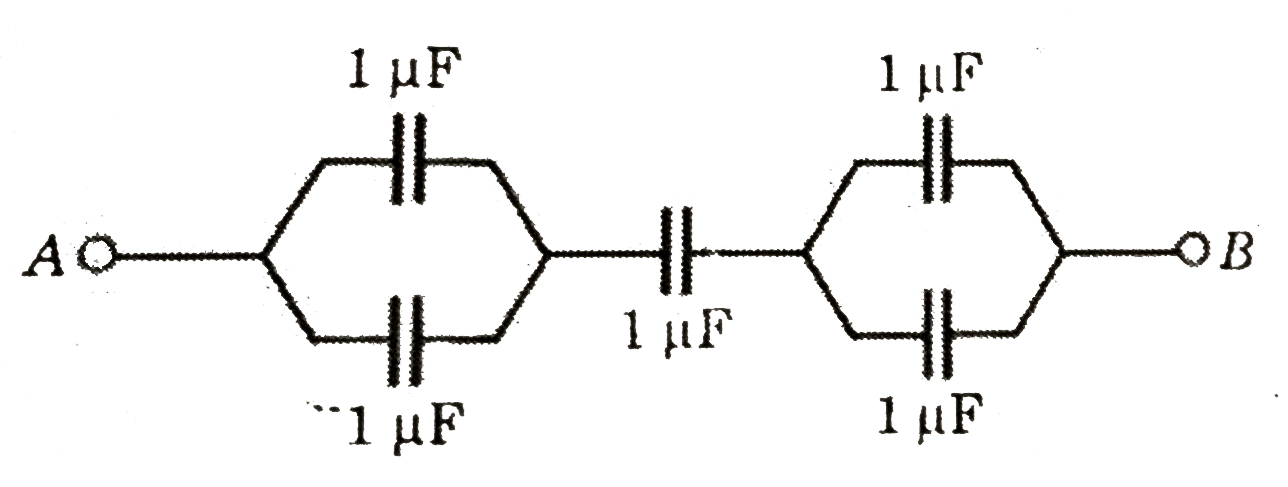
Calculate the equivalent capacitance between points A and B of the combination shown in figure.
View SolutionFind the equivalent capacitance between the point A and B in figure .

View SolutionFor the circuit, the equivalent capacitance between P and Q is
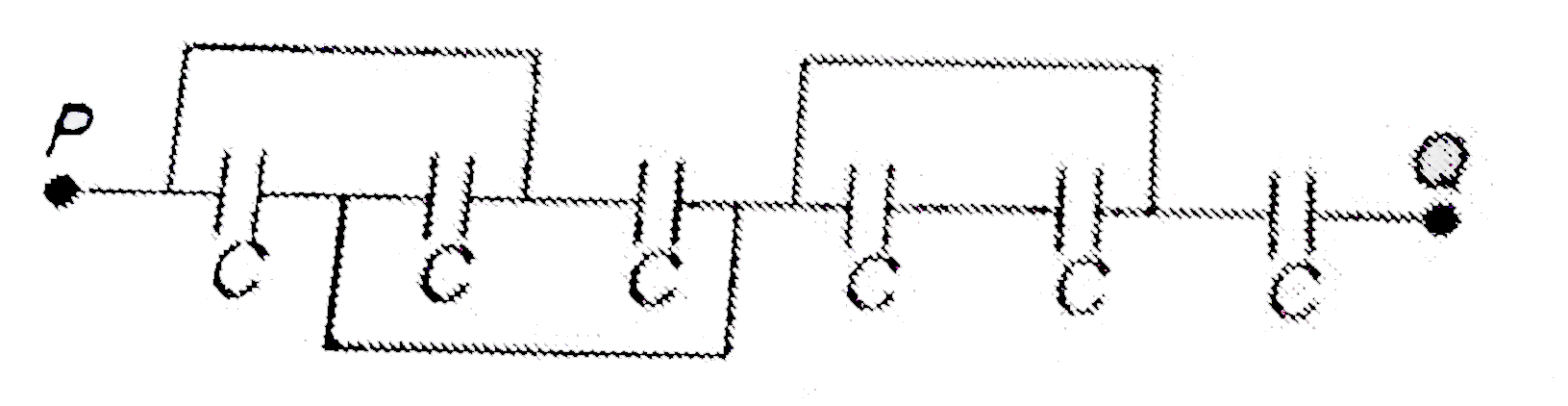
View Solution