A large ballon of volume 1425m3 is used to lift a payload of 400 kg. Assuming that the ballon maintains constant radius as it rises. How high does it rise? (TakeY0=8000m and ρHe=0.18kgm−3)Solution in Punjabi
Step by step video & image solution for A large ballon of volume 1425 m^3 is used to lift a payload of 400 kg. Assuming that the ballon maintains constant radius as it rises. How high does it rise? (Take Y_0 = 8000 m and rho_(He) = 0.18 kg m^-3) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Answer the following :- You can shield a charge from electrical forces by putting it inside a hollow conductor. Can you shield a body from the gravitational influence of nearby matter by putting it inside a hollow sphere or by some other means ?
View SolutionExplain the term viscosity.
View SolutionThe ballon the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distnce does the ballon descend? Mass of the ballon =M mass of the monkey =m and the length of the rope ascended by the monkey =L
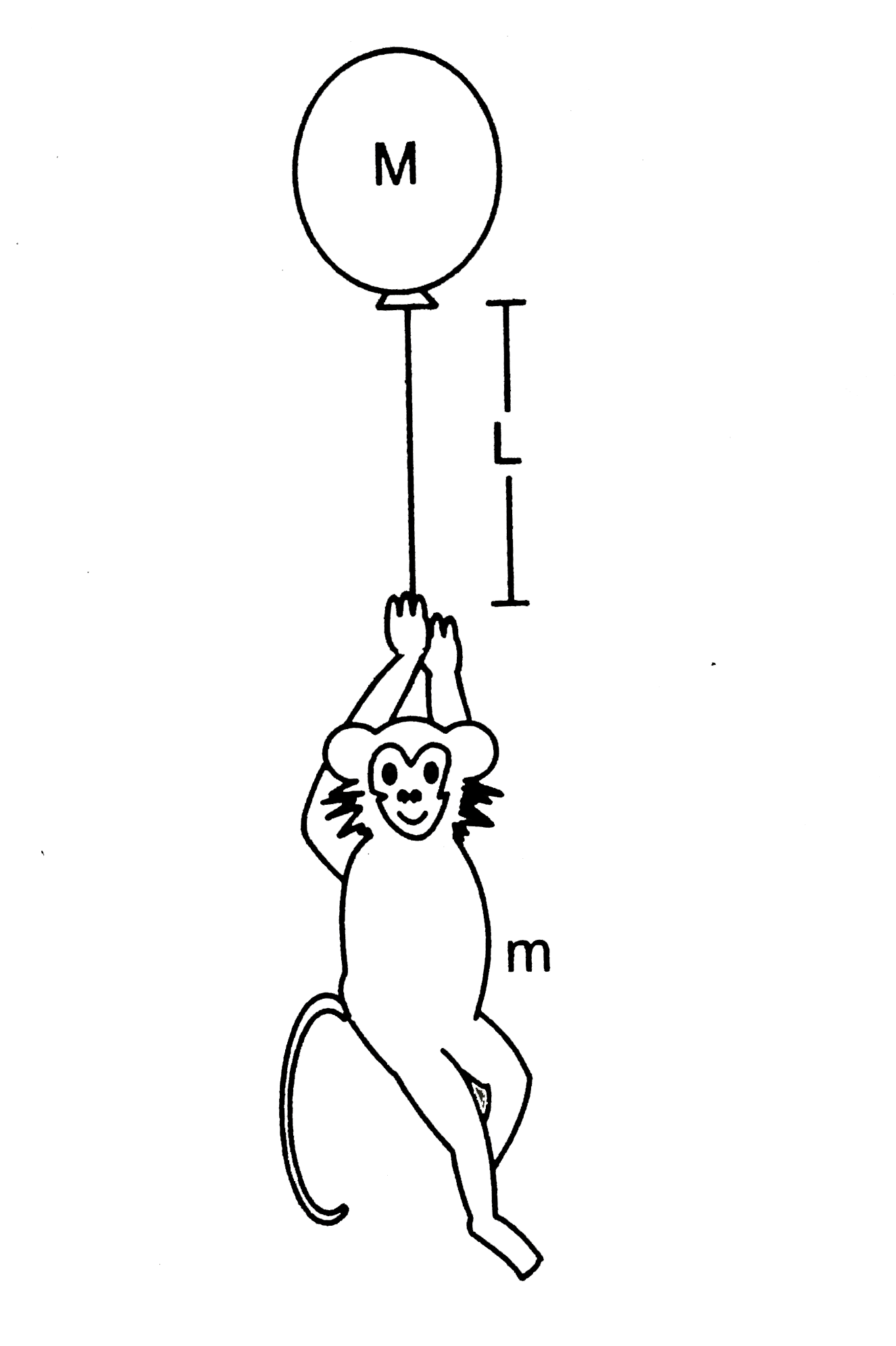
View SolutionNASA is experimenting with balloons for use on ultralong duration (100 days) flight around the Earth. Consider a balloon that has the shape of a cylindrical chamber which is 35 m tall with 30 m radius, and is made of extremely light plastic. If our model cylindrical balloon is filled with helium gas, what is the mass of the maximum payload it could lift from the Earth's surface? (Given ρair=1.29kgm3. ρHe)=0.18kgm3. Why would NASA design the balloon so large?
View Solution(a) It is known that density rho of air decrease with height y(in metres ) as rho =rho_(0)e^(-y//y_(0)) where rho_(0)=1.25kgm^(-3) is the density at see level , and y_(0) is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmospere remians a constant (isothermal conditions). Also assume that the value of g remains constant. (b) A large He balloon of volume 1425m^(3) is used to lift a payload of 400g . Assume that the balloon maintains constant radius as it rises. How high does it rise? [take y_(0)=800m and rho_(He) = 0.18kg//m^(3) ].
View Solution(a). It is known that density rho of air decreases with height y as rho=rho_(0)e^(-y//y(_o)) ltb rgt where p_(o)=1.25kgm^(-3) is the density at sea level, and y_(o) is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant (b). A large He balloon of volume 1425m^(3) is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise? [take y_(o)=8000m and rho_(He)=0.18kgm^(-3) ]
View SolutionRam took an empty ballon of mass 5 g and filled it with air. He then measured the mass of ballon filled with air tube to be 5.05 g. He considered the density of the air filled inside th ballon as 1.5 kg m−3 and found the volume of air present inside the ballon. Find his answer.
View Solution1425m3 आयतन का हीलियम से भरा कोई बड़ा गुब्बारा के किसी पेलोड ( m= 400 kg) को उठाने के काम में लाया जाता है | यह मानते हुए की ऊपर उठते समय गुब्बारे की त्रिज्या नियत रहती है, गुब्बारा कितनी अधिकतम ऊँचाई तक ऊपर उठेगा ? घनत्व ρ ऊँचाई y ( मीटरों में ) के साथ इस सम्बन्ध के अनुसार घटता है -
ρ=ρ0e−y/y0 ,[y0=8000m तथाρHe=0.18kg m−3 लीजिए|]
View SolutionIt is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y0
where ρ0=1.25kgm−3 is the density at sea level. And y0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
A large He balloon of volume 1425m3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View SolutionIt is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y0
where ρ0=1.25kgm−3 is the density at sea level. And y0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
A large He balloon of volume 1425m3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View SolutionIt is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y0
where ρ0=1.25kgm−3 is the density at sea level. And y0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant.
A large He balloon of volume 1425m3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View SolutionIt is known that density rho of air decreases with height y as rho=rho_0e^(-y//y_0) where rho_0=1.25 kg m^-3 is the density at sea level. And y_0 is a constant . This density variation is called the law of atmosphere. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant. A large He balloon of volume 1425 m^3 is used to lift a payload of 400kg.Assume that the balloon maintains constant radius as it rises. How high does it rise?
View Solution(a). It is known that density ρ of air decreases with height y as
ρ=ρ0e−y/y(_o) ltb rgt where po=1.25kgm−3 is the density at sea level, and yo is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions). Also assume that the value of g remains constant
(b). A large He balloon of volume 1425m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[take yo=8000mandρHe=0.18kgm−3]
View SolutionThe hot air ballon rises because it is
View SolutionIt is known that density rho of air decreases with height y as -y//y_(0) rho=rho_(o)e where rho_(o)=1.25kgm^(-3) is the density at sea level and y_(o) is a constant . This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of atmosphere remains a constant (isothermal conditions).Also assume that the value of g remains constant. (b) A large He balloon of volume 1425m^(3) is used to lift a payload of 400 kg . Assume that the balloon maintains constant radius as it rises . How high does it rise ? (y_(o)=8000mandrho_(He)=0.18kgm^(-3)) .
View SolutionThe ballon the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distnce does the ballon descend? Mass of the ballon =M mass of the monkey =m and the length of the rope ascended by the monkey =L
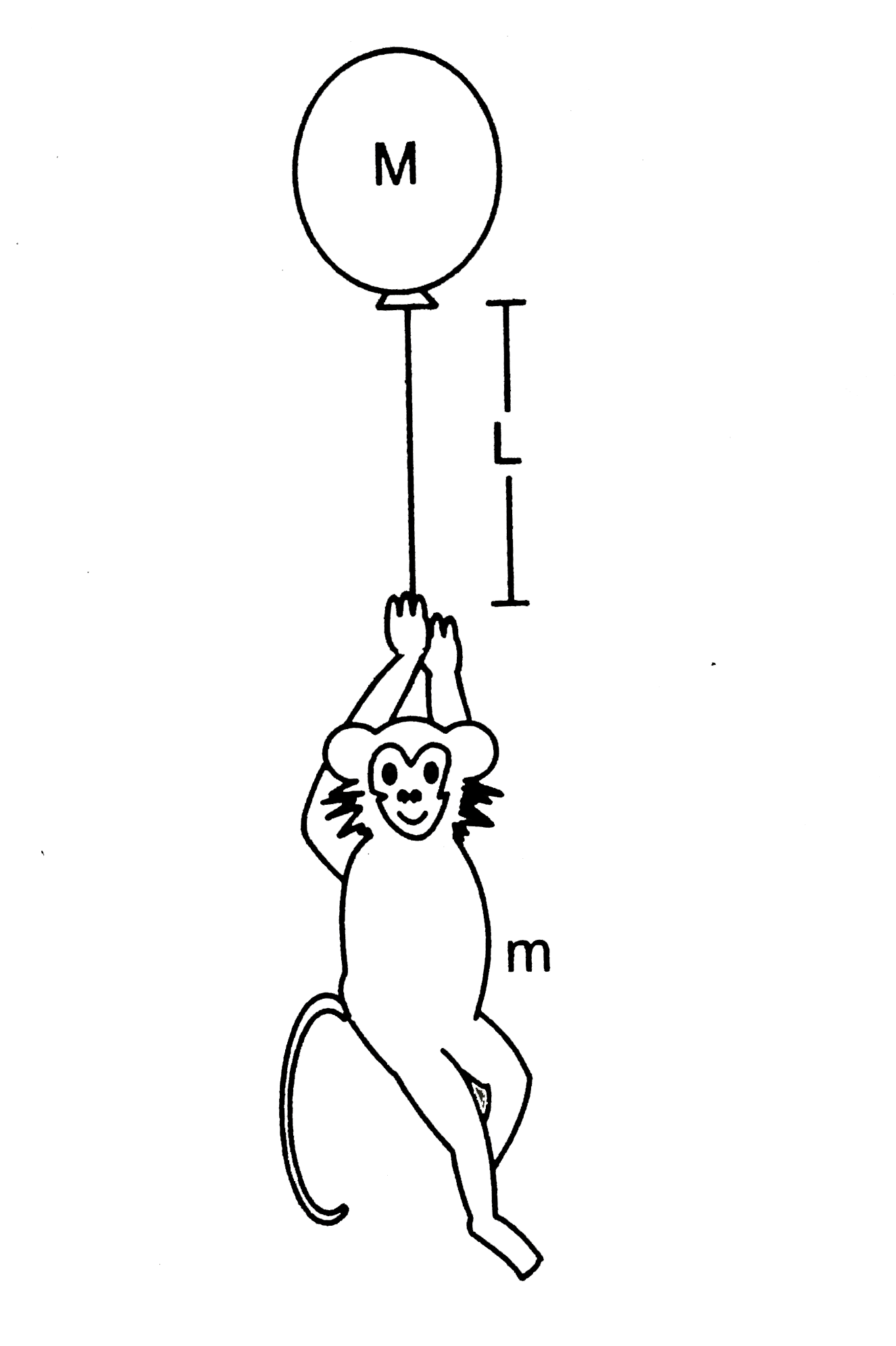
View Solution
