The ballon the light rope and the monkey shown in figure are at rest in the air. If the monkey reaches the top of the rope, by what distnce does the ballon descend? Mass of the ballon =M mass of the monkey =m and the length of the rope ascended by the monkey =L
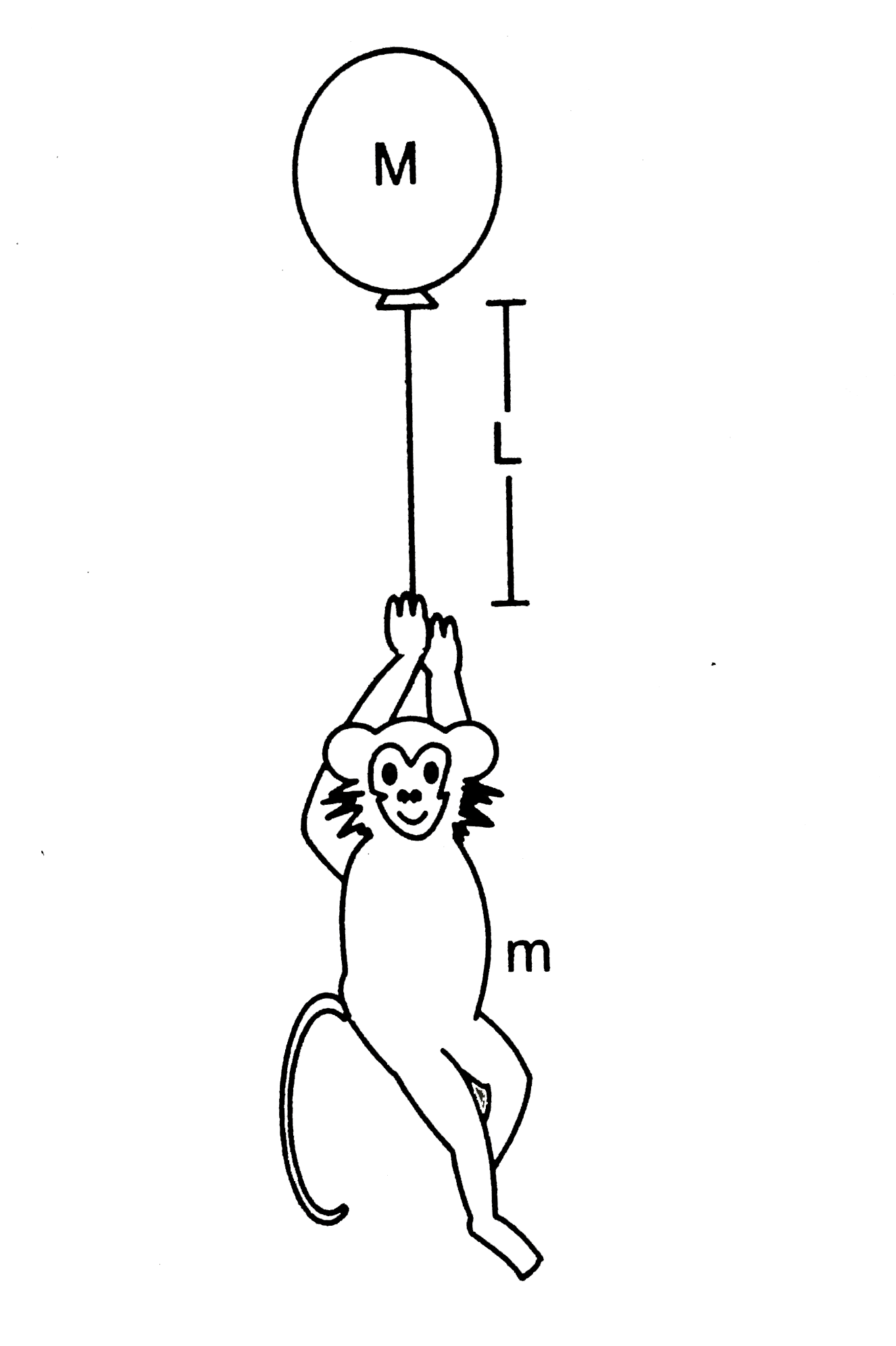
Initially the monkey and balloon are at rest. Os, the CM is at P.
When the monkey descends through a distance L the cm. will shift.

t0=m+L+M×0M+m
=mLM+momP
So, the balloon descenes through a distance mLM+m
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective 2
11 Videos
- CALORIMETRYBOOK - HC VERMACHAPTER - CALORIMETRYEXERCISE - Exercises
18 Videos
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Exercises
30 Videos
Similar Questions
A 20kg monkey has a firm hold on a light rope that passes over a frictionless pulley and is attached to a 20cm bunch if bananas. The monkey looks upwards , sees the bananas and starts to climb the rope to get them.
(a) As the monkey climbs ,do the bananas move up , move down or remain at rest?
(b) As the monkey climbs ,does the distance between the lonkey and the banana decrease, increase or remain contact?
(c) The monkey releases her hold on the rope .What happens to the distance between the monkey and the bananas while she is falling ?
(d) Before reaching the ground , the monkey grabs the rope of stop har fall. What do the bananas do?
View SolutionIf a monkey moves upward with respect to the rope with acceleration g/2 then acceleration of block, if masses of block and monkey are same
View Solution
Knowledge Check
A balloon of mass M with a light rope having monkey on the rope is in equilibrium. If the monkey starts moving up with acceleration a w.r.t. rope . Then the acceleration of cenre of mass of the system is
 Aa(M−m)(M+m)BZeroCaDaMm
Aa(M−m)(M+m)BZeroCaDaMmAs shown in figure a monkey of 20g mass is holding a light rope that passes over a frictionless pulley. A bunch of bananas of the same mass is tied to the other end of rope. Inorder to get access to the bunch the monkey starts climbing the rope. The distance between the monkey and the bananas is
 ADecreasingBIncreasingCUnchangedDNothing can be stated
ADecreasingBIncreasingCUnchangedDNothing can be stated
A monkey of massm clings to a rope slung over a fixed pulley. The opposite end of the rope is tied to a weight of
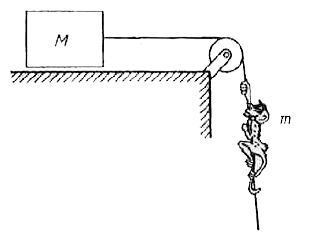
mass M lying on a horizontal plat (Fig.). Neglecting friction find the acceleration of both bodies (relative to the plate) and the tension of the rope for the three cases:
(1) the monkey does not move with respect to the rope,
(2) the monkey moves upwards with respect to the rope with acceleration b,
(3) the monkey moves downwards with respect to the rope with an acceleration b.
View SolutionIn the arrangement shown in the fig. a monkey of mass M keeps itself as well as block A at rest by firmly holding the rope. Rope is massless and the pulley is ideal. Height of the monkey and block A from the floor is h and 2h respectively [h = 2.5 m]
(a) The monkey loosens its grip on the rope and slides down to the floor. At what height from the ground is block A at the instant the money hits the ground?
(b) Another block of mass equal to that of A is stuck to the block A and the system is released. The monkey decides to keep itself at height h above the ground and it allows the rope to slide through its hand. With what speed will the block strike the ground?
(c) In the situation described in (b), the monkey decides to prevent the block from striking the floor. The monkey remains at height h till the block crosses it. At the instant the block is crossing the monkey it begins climbing up the rope. Find the minimum acceleration of the monkey relative to the rope, so that the block is not able to hit the floor. Do you think that a monkey can climb with such an acceleration? (g=10ms−2)

View SolutionConsider the situation as shown in the figure. The boy of mass M holds the light rope and the system is at rest. If m is mass of the box, find the force exerted by the boy on the rope and contact force beteween the boy and the box.

View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View SolutionA monkey of mass m climbs up to a rope hung over a fixed pulley. The opposite end of the rope is tied to a weight of mass M lying on a horizontal plane. Neglecting the friction, find the acceleration of both the bodies (relative to the plane) and the tension of the rope for the three cases:
(i) The monkey does not move with respect to the rope
(ii) The monkey moves upwards with respect to the rope with acceleration a.
(iii) The monkey moves downwards with respect to the rope, with acceleration a.
View SolutionTwo ladders are hanging from ands of a light rope passing over a light and smooth pulley. A monkey of mass 2m hangs near the bottom of one ladder whose mass is M-2m. Another monkey of mass m hangs near the bottom of the other ladder whose mass is M-m. The monkey of mass 2m moves up a distance l with respect to the ladder. The monkey of mass m moves up a distance l/2 with respect to the ladder. The displacement of centre of mass of the system is kml4M. Find the value of k.

View Solution
