WORK DONE IN ADIABATIC PROCESS
A
nR(T1−T2)γ
B
nR(T1−T2)γ−1
C
nγ(T1−T2)R
D
γ(T1−T2)Rn
Video Solution
Text Solution
The correct Answer is:B
W=∫V2V1PdV=K∫V2V1dVVγ
K[V−γ+1−γ+1]V2V1
=K1−γ[1Vγ−12−1Vγ−11]
W=11−γ[P2Vγ1Vγ−12−P1Vγ1Vγ−11]
=11−γ[P2V2−P1V2]
=nR1−γ(T2−T1)=nR(T1−T2)(γ−1)
[∴P1V1=nRT1andP2V2=nRT2]
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If WABC is the work done in process A→B→C and WDEF is work done in process D→E→F as shown in the figure, then
 A(a) |WDEF|>|WABC|B(b) |WDEF|<|WABC|C(c) |WDEF|<|WABC|D(d) WDEF=−WABC
A(a) |WDEF|>|WABC|B(b) |WDEF|<|WABC|C(c) |WDEF|<|WABC|D(d) WDEF=−WABCA monoatomic ideal is used as the working substance for the carnot cycle shown in the figure. Processes AB and CD are isothermal, while processes BC and DA are adiabatic. During process AB, 400 J of work is done by the gasd on the surroundings. How much heat is expelled by the gas during process CD?
 A1600 JB400 JC200 JD100 J
A1600 JB400 JC200 JD100 JIf a pari of inear equations is consistent then the lines represented by then are
A3 RTBRTC6 RTD2 RT
Work Done In Isothermal Reversible Process
View SolutionWork Done In Irreversible Process And Free Expansion
View SolutionFind work in the given cycle, If AB is isothermal process and CA is adiabatic.
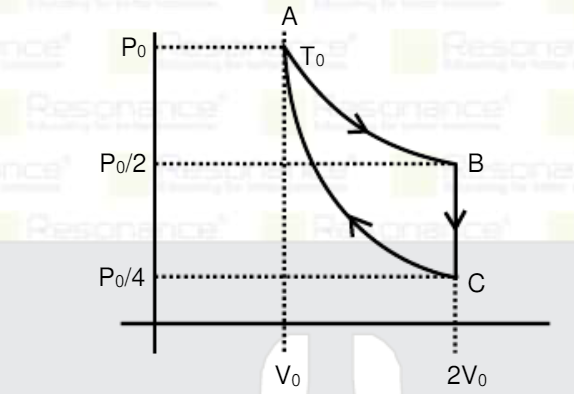
View SolutionAn ideal monatomic gas expands to twice its volume. If the process is isothermal, the magnitude of work done by the gas is W1. If the process is adiabatic, the magnitude of work done by the gas is Wa . Which of the following is true ?
View Solution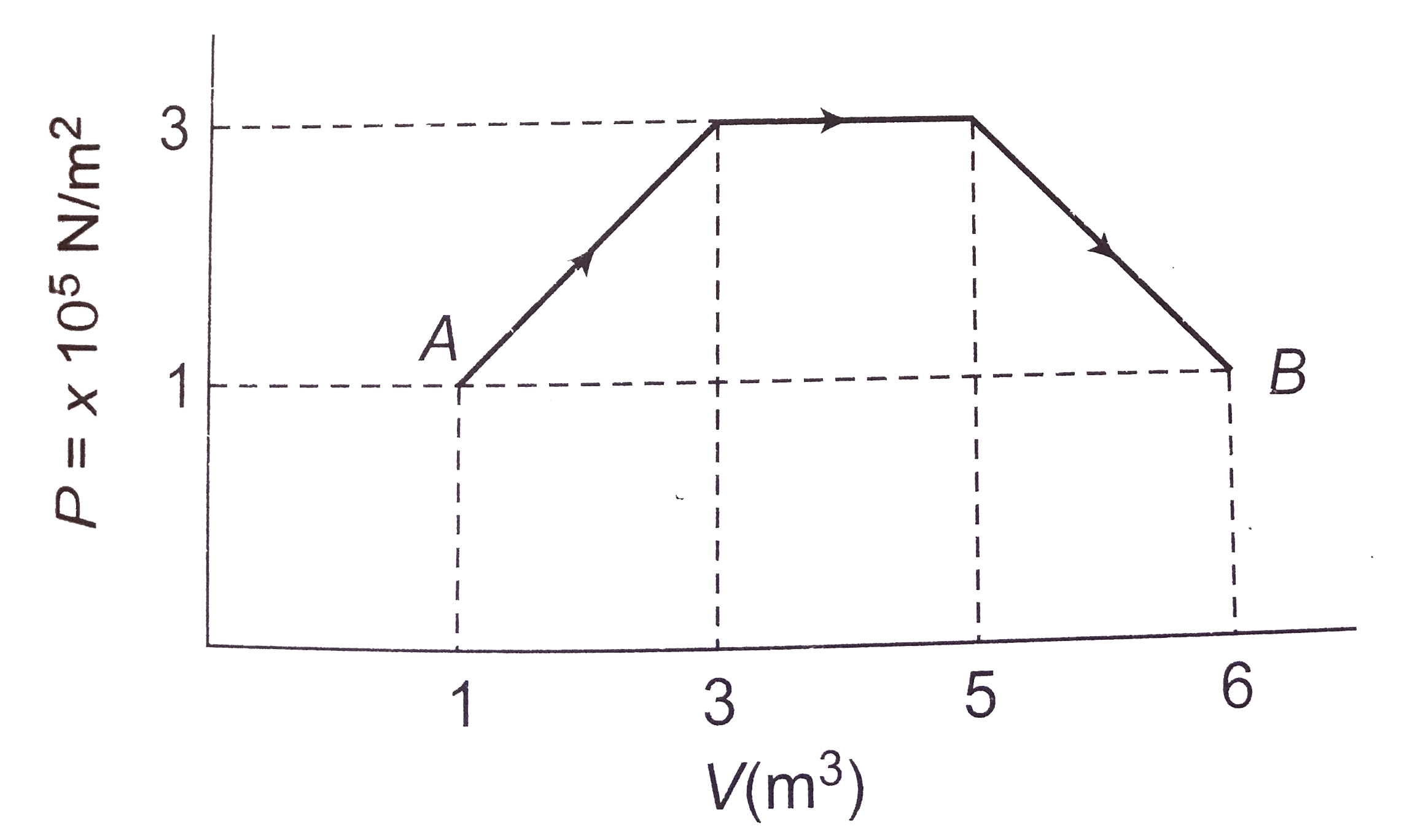
The work done in the process AB is
View Solution
