Calculate the time period of the oscillation of a particle of mass m moving in the potential defined as Ux={12kx2,x<0mgx,x>0
π√mk+2√2Eg2m, where E is g.m the total energy of the particle.
Topper's Solved these Questions
- OSCILLATIONSBook:NCERT TAMILChapter:OSCILLATIONSExercise:EVALUATION(I. MULTIPLE CHOICE QUESTIONS)
Explore 15 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBook:NCERT TAMILChapter:NATURE OF PHYSICAL WORLD AND MEASUREMENTExercise:EXERCISE (V. Conceptual Questions)
Explore 5 Videos
- PHYSICAL WORLD Book:NCERT TAMILChapter:PHYSICAL WORLD Exercise:EXERCISES
Explore 15 Videos
Similar Questions
When a particle of mass m moves on the x-axis in a potential of the form V(x)=kx2 it performs simple harmonic motion. The correspondubing time period is proprtional to √mh, as can be seen easily using dimensional analusis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of x=0 in a way different from kx2 and its total energy is such that the particle does not escape toin finity. Consider a particle of mass m moving on the x-axis. Its potential energy is V(x)=ax4(a>0) for |x| neat the origin and becomes a constant equal to V0 for |x|impliesX_(0)(seefigure).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_CHMO_C10_033_Q01.pngwh=80%mx-autosty≤=background:white;>.<br>Theae≤rationofthisparti≤for|x|gtX_(0)is<br>(a)∝rtional→V_(0)
(b) proportional to.
View SolutionA particle is moving in a potential region defined by U=K(x2+y2+z2). Calculate the force acting on the particle.
View Solution
Knowledge Check
When a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0
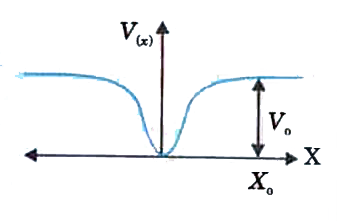
For periodic motion os small amplitude A . The time periodic T of this particle is proportional toAA√mαB1A√mαCA√αmD1A√αmWhen a particle of mass m moves on the X-axis in a potential of the form V(x)=kx2, it performs simple harmonic motion. The corresponding time period is proportional to
√mk, as can be seen easily using dimensional analysis.
However, the motion of a particle can be periodic even when its potential energy increases on both sides of x = 0 in a way different from kx2 and its total energy is such that the particle does not escape to infinity. Consider a particle of mass m moving on the X-axis. Its potential energy is V(x) =ax2(a>0) for |x| near the origin and becomes a constant equal to V0 for |x|≥X0

The acceleration of this particle for |X|>X0 isAproportional to (v0mX0)Bpropotinal to √V0mX0Cproportional to V0DZeroIf f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x−1,x<014,x=0x2,x>0
Alimx→0+f(x)=1Blimx→0−f(x)=1Cf(x) is discontinuous atx=0Df(x) is continuous atx=0
The function f is defined as :
f(x)=⎧⎪⎨⎪⎩1,x>00,x=0−1,x<0
The range of f is :
View SolutionThere exist a potential field
U(x)= U0(1−cosαx) .where
U0&α are constants. A mass m is
located in this field. The time
period of oscillation of this mass is
found to be proportional to
maUb0αc. Now find the product of abc=?
View SolutionThe potential energy of a particle of mass 'm' situated in a unidimensional potential field varies as U(x)=U0[1−cos(ax2)], where U0 and a are positive constant. The time period of small oscillations of the particle about the mean position-
View SolutionIf a function f(x) is defined as f(x)=⎧⎪⎨⎪⎩−x,x<0x2,0≤x≤1x2−x+1,x>1 then
View SolutionThe potential energy of a particle of mass 'm' situated in a unidimensional potential field varies as U(x)=U0[1−cos(ax2)], where U0 and a are positive constant. The time period of small oscillations of the particle about the mean position-
View Solution
