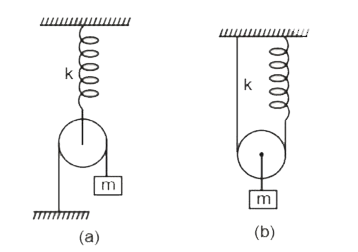
Compute the time period for the following system if the block of mass m is slightly displaced vertically down from its equilibrium position and then released. Assume that the pulley is light and smooth, strings and springs are light.

Case(a)
Pulley is fixed rigidly here. When the mass displace by y and the spring will also stretch by y. Therefore, F = T = ky
T=2π√mk
Case(b)
Mass displace by y, pulley also displaces by y. T = 4ky .
T=2π√m4k
Topper's Solved these Questions
- OSCILLATIONSBOOK - NCERT TAMILCHAPTER - OSCILLATIONSEXERCISE - EVALUATION(I. MULTIPLE CHOICE QUESTIONS)
15 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - EXERCISE (V. Conceptual Questions)
5 Videos
- PHYSICAL WORLD BOOK - NCERT TAMILCHAPTER - PHYSICAL WORLD EXERCISE - EXERCISES
15 Videos
Similar Questions
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionIn the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
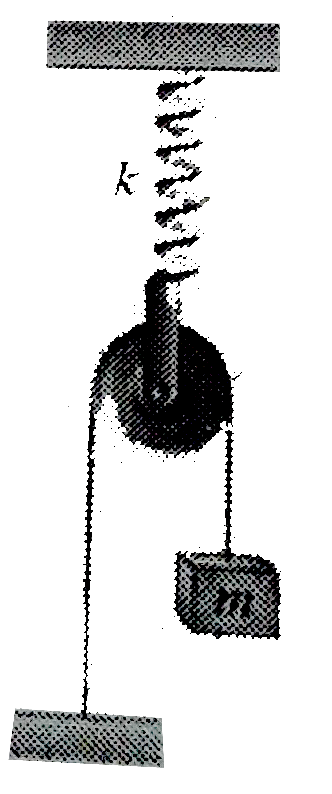 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mK
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
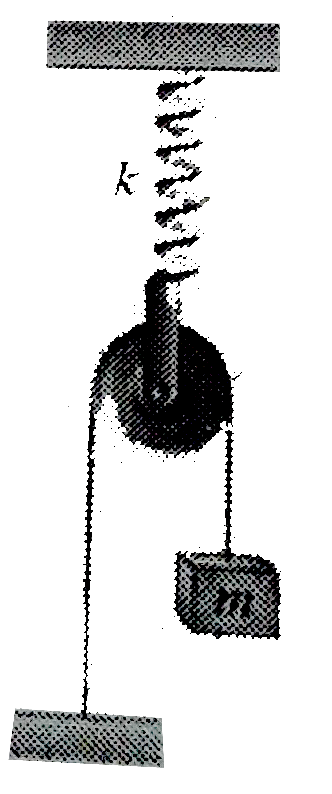
View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then reelased for the system shown in figure.
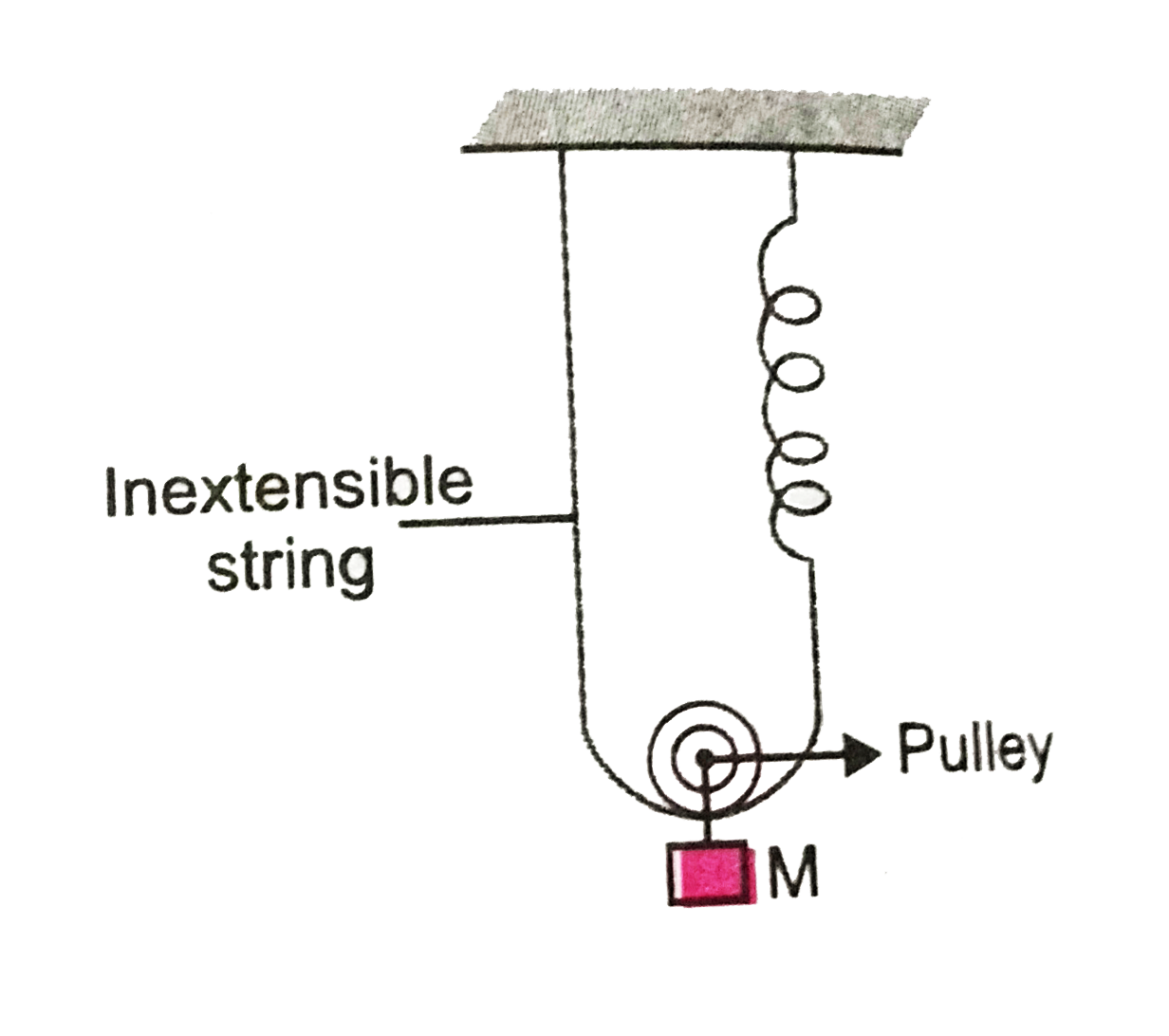
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

View Solution
