Apply Newton’s second law to a mango hanging from a tree. (Mass of the mango is 400 gm)

Text Solution

Verified by Experts

Note: Before applying Newton’s laws, the following steps have to be followed:
1) Choose a suitable inertial coordinate system to analyse the problem. For most of the cases we can take Earth as an inertial coordinate system.
2) Identify the system to which Newton’s laws need to be applied. The system can be a single object or more than one object.
3) Draw the free body diagram.
4) Once the forces acting on the system are identified, and the free body diagram is drawn, apply Newton’s second law. In the left hand side of the equation, write the forces acting on the system in vector notation and equate it to the right hand side of equation which is the product of mass and acceleration. Here, acceleration should also be in vector notation.
5) If acceleration is given, the force can be calculated. If the force is given, acceleration can be calculated.

By following the above steps:
We fix the inertial coordinate system on the ground as shown in the figure

The forces acting on the mango are
i) Gravitational force exerted by the Earth on the mango acting downward along negative y axis
ii) T ension (in the cord attached to the mango) acts upward along positive y axis.
The free body diagram for the mango is shown in the figure.

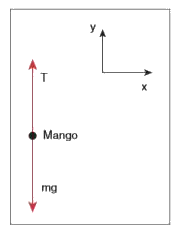
${\to F}_{x} = m g (- ˆ j) = - m g ˆ j$
Here, mg is the magnitude of the gravitational force and $(- ˆ j)$ represents the unit vector in negative y direction.
$\to T = T ˆ j$
Here T is the magnitude of the tension force and $(ˆ j)$ represents the unit vector in positive y direction.
${\to V}_{net} = {\to F}_{g} + \to T = - m g ˆ j + T \to j = (T - m g) ˆ j$
From Newton’s second law ${\to F}_{net} = m \to a$
Since the mango is at rest with respect to us (inertial coordinate system) the acceleration is zero $(\to a = 0)$
So ${\to F}_{net} = m \to a = 0$
$(T - m g) ˆ k = 0$
By comparing the components on both sides of the above equation, we get T mg −= 0
So the tension force acting on the mango is given by T mg
Mass of the mango m = 400g and $g = 9.8 m s^{- 2}$
Tension acting on the mango is $T = 0.4 \times 9.8 = 3.92 N$

Updated on:21/07/2023