An object of mass m is projected from the ground with initial speed $v_{0}$
Find the speed at height h.

Text Solution

Verified by Experts

Since the gravitational force is conservative, the total energy is conserved throughout the motion.

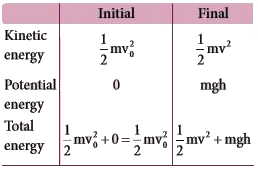
Final values of potential energy, kinetic energy and total energy are measured at the height h.
By law of conservation of energy, the initial and final total energies are the same.
$\frac{1}{2} m v_{0}^{2} = \frac{1}{2} m v^{2} + m g h$
$v_{0}^{2} = v^{2} + 2 g h$
$v = \sqrt{v_{0}^{2} - 2 g h}$
Note that in section (2.11.2) similar result is obtained using kinematic equation based on calculus method. However, calculation through energy conservation method is much easier than calculus method.

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m is projected from the surface of earth with a speed $V_{0} (V_{0} <$ escape velocity). Find the speed of particle at height $h = R$ (radius of earth). (Take, $R = 6400 k m$ and $g = 9.8 m / s^{2})$
A $\sqrt{g R}$
B $\sqrt{v_{0}^{2} - 2 g R}$
C $\sqrt{v_{0}^{2} - g R}$
DNone of these
Question 2 - Select One
Two particles of equal mass 'm' are projected from the ground with speed $v_{1}$ and $v_{2}$ at angles $θ_{1}$ and $θ_{2}$ at the same times as shown in figure. The centre of mass of the two particles.

Awill move in a vertical line if $v_{1} tan θ = v_{2} {tan θ}_{2}$
Bwill move in a vertical line if $v_{1} sin θ = v_{2} {sin θ}_{2}$
Cwill move In a vertical line if $v_{1} {cot θ}_{1} = v_{2} {cot θ}_{2}$
Dwill move in a vertical line if $v_{1} {cos θ}_{1} = v_{2} {cos θ}_{2}$
Question 3 - Select One
A particle is projected from the ground with an initial speed of v at an angle $θ$ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
A $\frac{v}{2} \sqrt{1 + 2 {cos}^{2} θ}$
B $\frac{v}{2} \sqrt{1 + 2 {cos}^{2} θ}$
C $\frac{v}{2} \sqrt{1 + 3 {cos}^{2} θ}$
D $v cos θ$

NCERT TAMIL-WORK, ENERGY AND POWER-EXAMPLE

Home
Ask Doubt
Profile