An object of mass 2 kg attached to a spring is moved to a distance x = 10 m from its equilibrium position. The spring constant k = 1 N m−1 and assume that the surface is frictionless.
When the mass crosses the equilibrium position, what is the speed of the mass?
Since the spring force is a conservative force, the total energy is constant. At x = 10 m, the total energy is purely potential.
E=U=12kx2=12×(1)×(10)2=50J
When the mass crosses the equilibrium position (x = 0), the potential energy
U=12×1×(0)=0J
The entire energy is purely kinetic energy at this position.
E=KE=12mv2=50J
The speed
v=√2KEm=√2×502=√50ms−1≈7.07ms−1
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE - MULTIPLE CHOICE QUESTIONS
15 Videos
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISE - IV. NUMERICAL PROBLEMS
5 Videos
- WORK, ENERGY AND POWERBOOK - NCERT TAMILCHAPTER - WORK, ENERGY AND POWEREXERCISE - EXERCISES (ADDITIONAL EXERCISES)
7 Videos
- WAVESBOOK - NCERT TAMILCHAPTER - WAVESEXERCISE - EVALUATION(IV. NUMERICAL PROBLEMS)
7 Videos
Similar Questions
A mass of 2 kg is attached to the spring constant 50Nm−1. The block is pulled to a distance of 5cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA block of mass one kg is fastened to a spring with a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. Write the expression for its x(t) and v(t).
View Solution
Knowledge Check
In the given figure, a mass M is attached to a horizontal spring which is fixed on one side to a rigid support. The spring constant of the spring is k. The mass oscillates on a frictionless surface with time period T and amplitude A. When the mass is in equilibrium position, as shown in the figure, another mass m is gently fixed upon it. The new amplitude of oscillation will be :
 AA√M−mMBA√MM+mCA√M+mMDA√MM−m
AA√M−mMBA√MM+mCA√M+mMDA√MM−mA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
Ax=0.05sin5t mBx=0.05cos5t mCx=0.5sin5t mDx=5sin5t m
A mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA mass of 2kg is attached to the spring of spring constant 50Nm−1. The block is pulled to a distance of 5 cm from its equilibrium position at x=0 on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the phase constant ϕ for the motion?
View SolutionA block whose mass m is 680g is fastened to a spring whose spring constant k is 65N/m. The block is pulled a distance x=11cm from its equilibrium position at x=0 on a frictionless surface and released from rest at t= 0.
What is the amplitude of the oscillation?
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
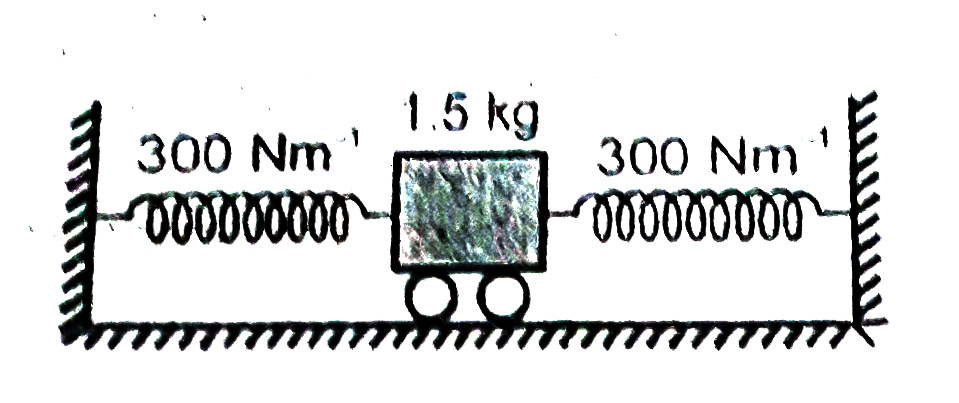
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximu speed of the trolley is
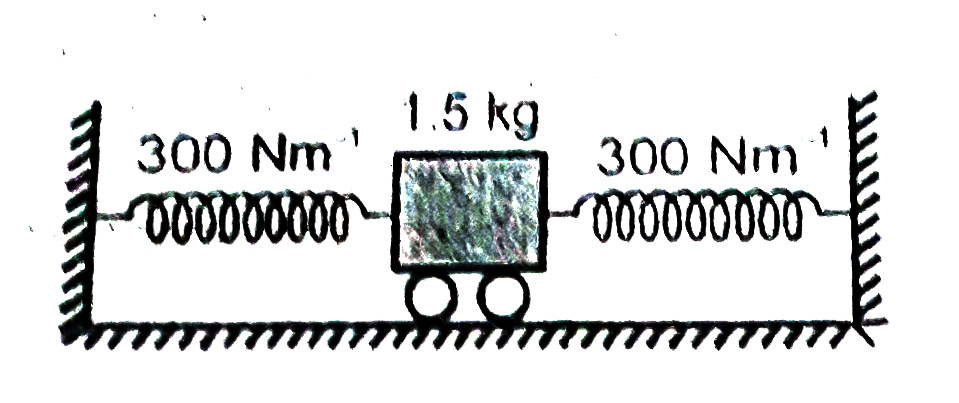
View Solution
