A particle which is constrained to move along x-axis, is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−kx+ax3. Here, k and a are positive constants. For x≥0, the functional form of the potential energy U(x) of the particle is
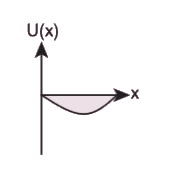
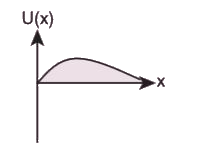
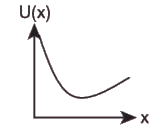
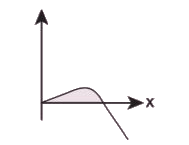
The correct Answer is:D
Topper's Solved these Questions
- WORK, ENERGY AND POWERBook:NCERT TAMILChapter:WORK, ENERGY AND POWERExercise:EXERCISE - IV. NUMERICAL PROBLEMS
Explore 5 Videos
- WORK, ENERGY AND POWERBook:NCERT TAMILChapter:WORK, ENERGY AND POWERExercise:EXAMPLE
Explore 36 Videos
- WAVESBook:NCERT TAMILChapter:WAVESExercise:EVALUATION(IV. NUMERICAL PROBLEMS)
Explore 7 Videos
Similar Questions
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with the distance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the particle is.
(a)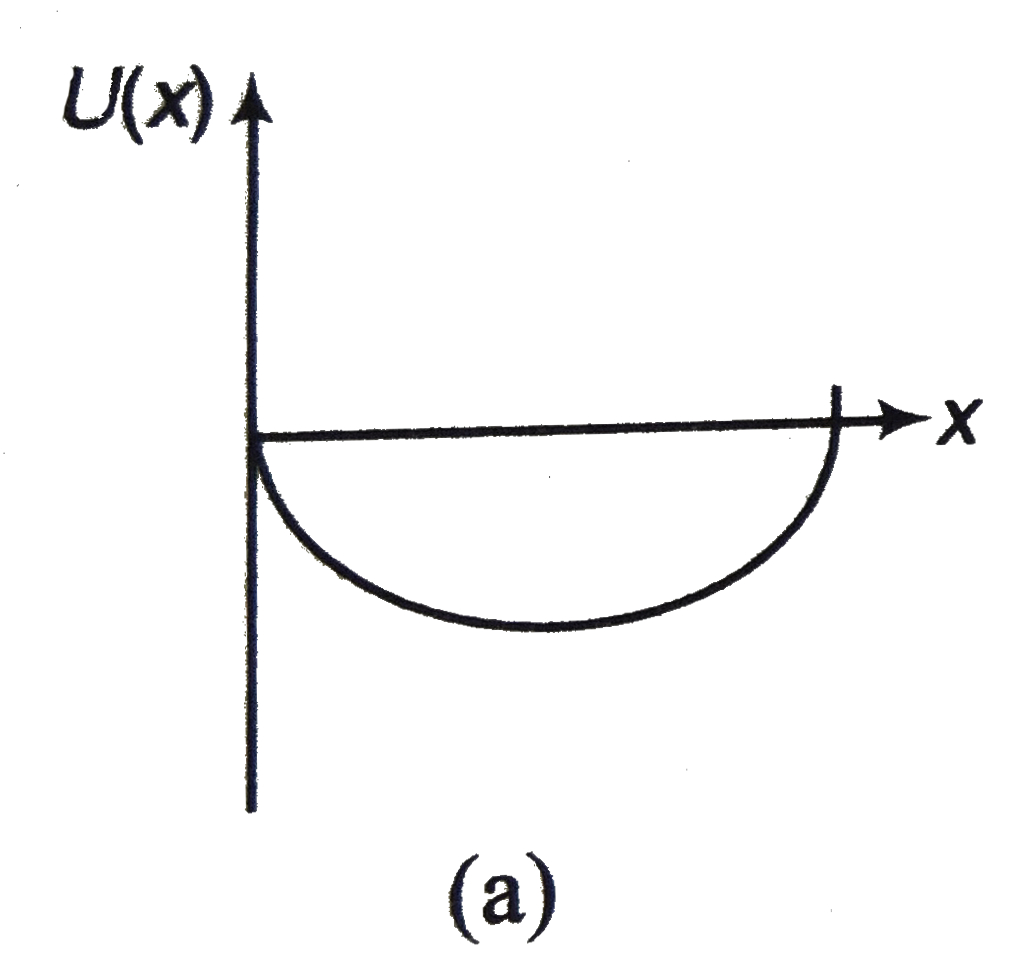 , (b)
, (b) 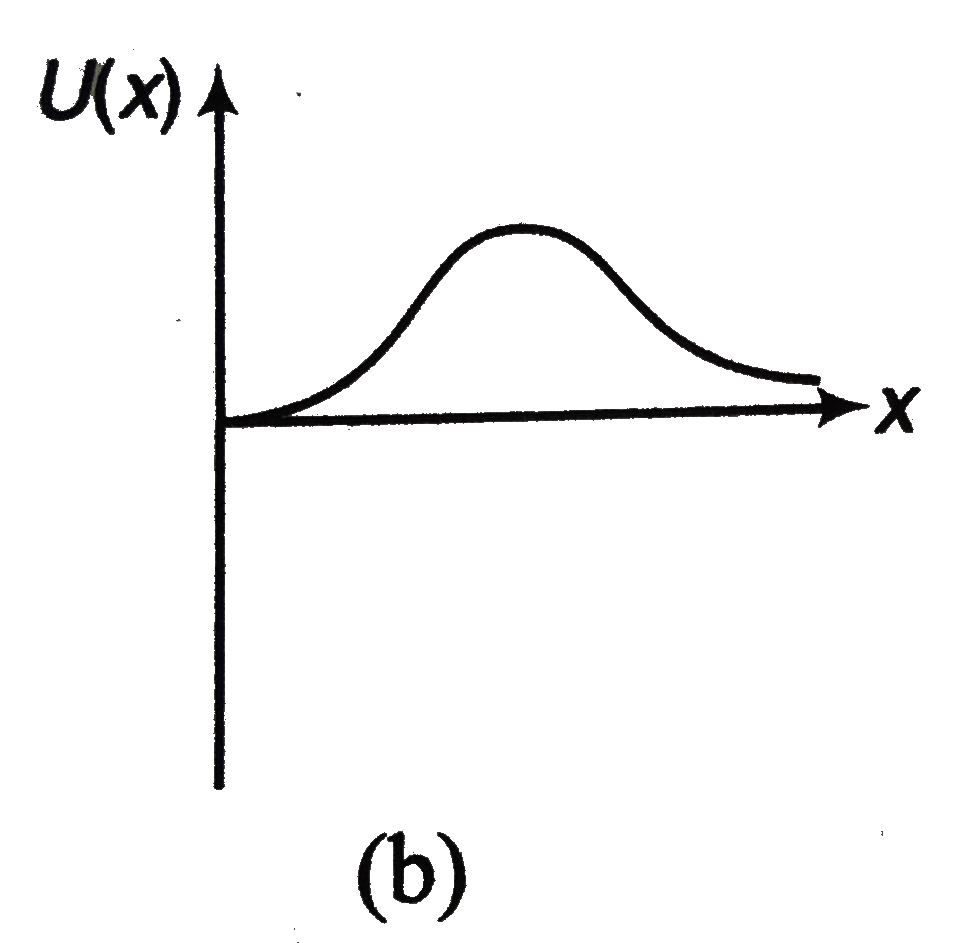 , (c)
, (c) 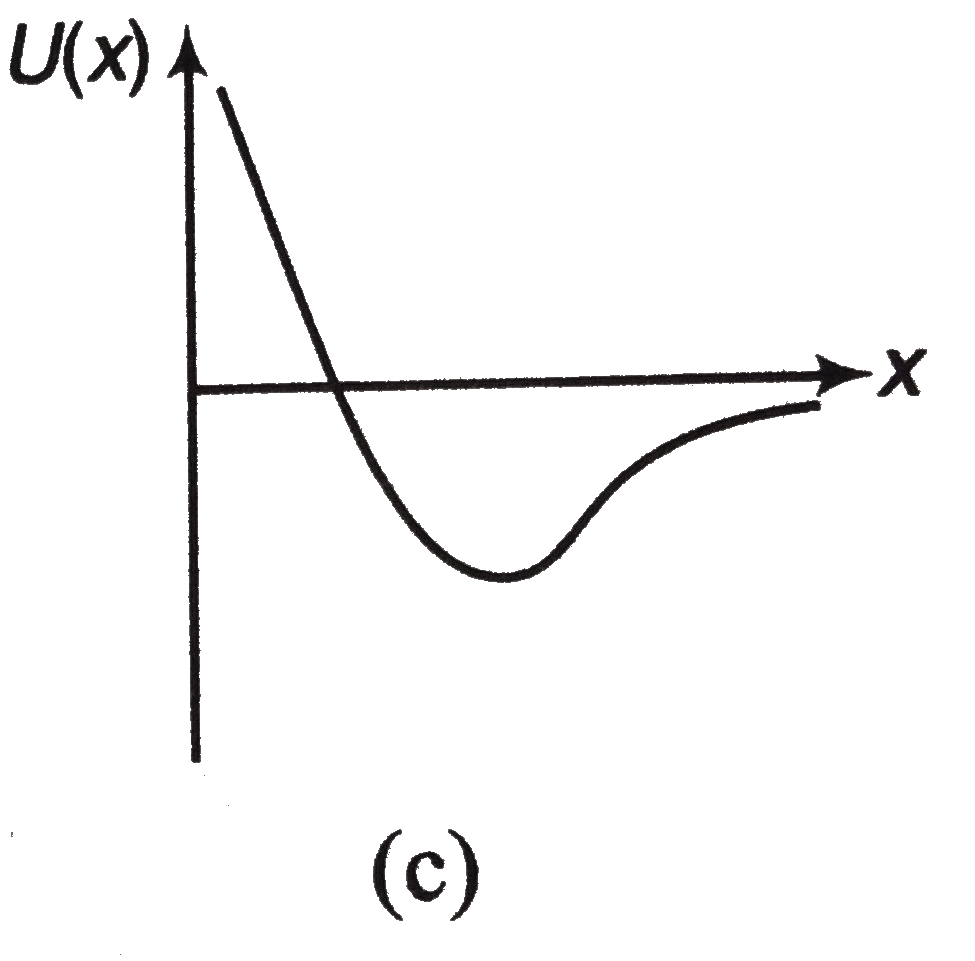 , (d)
, (d) 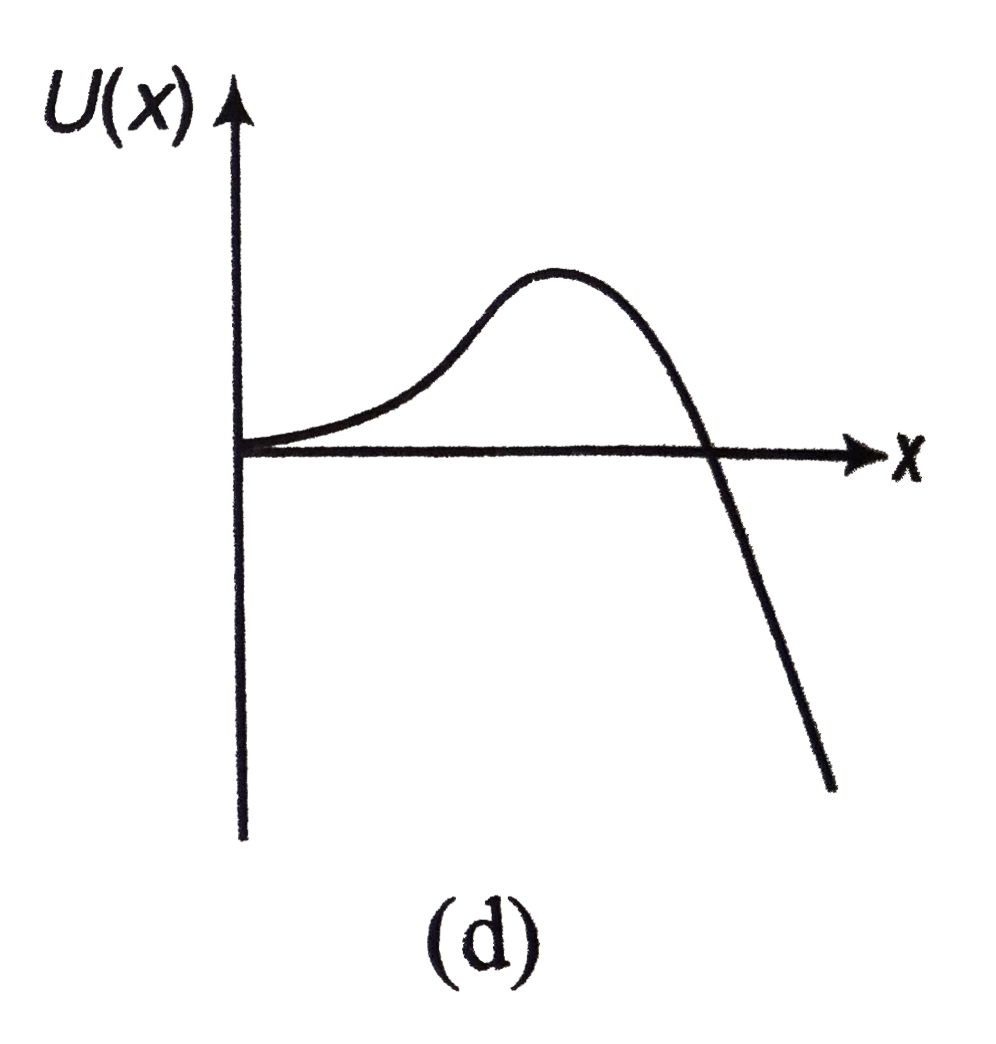 .
.
View SolutionA particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a) , (b)
, (b)  , (c)
, (c)  , (d)
, (d)  .
.
View Solution
Knowledge Check
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B C
C D
D
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B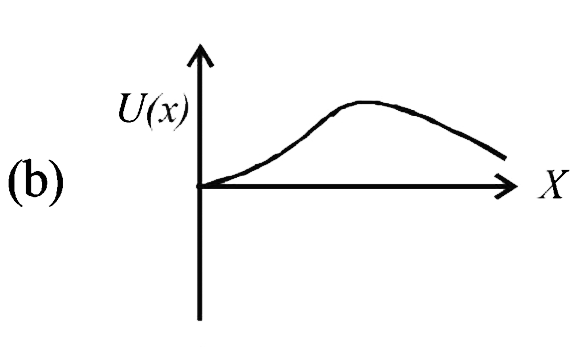 C
C D
D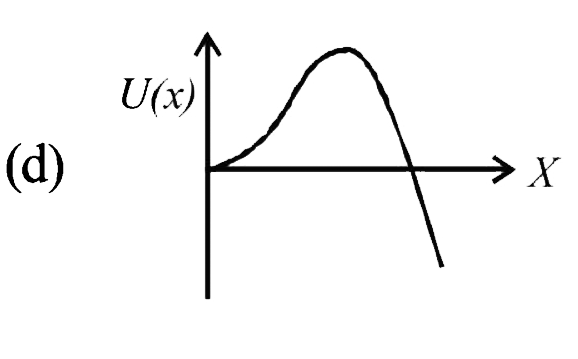
A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
A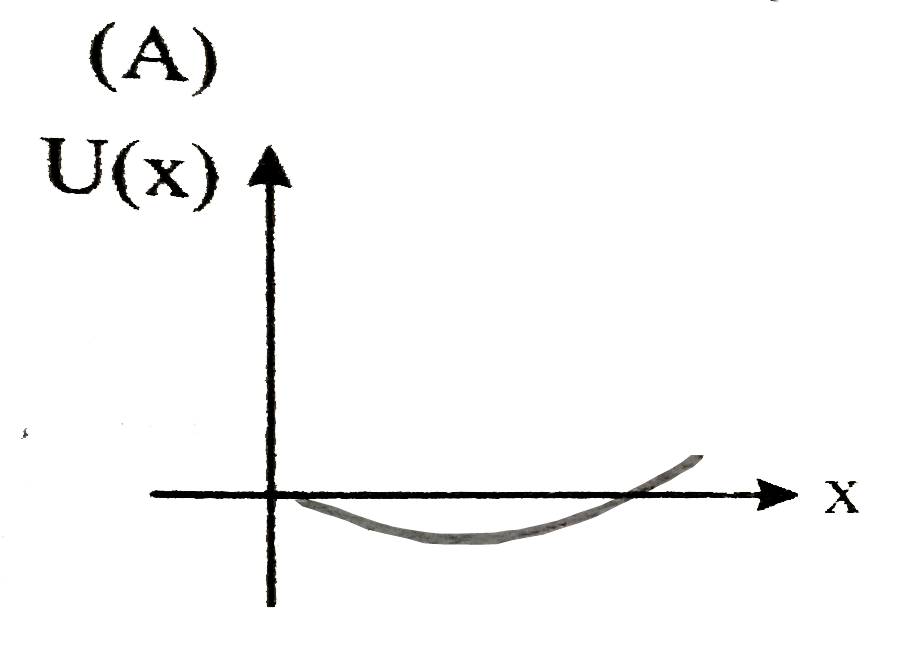 B
B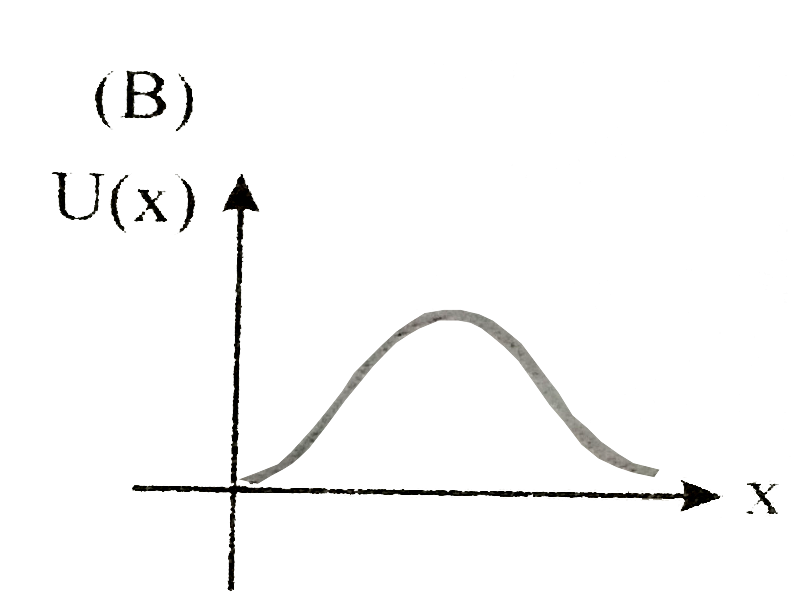 C
C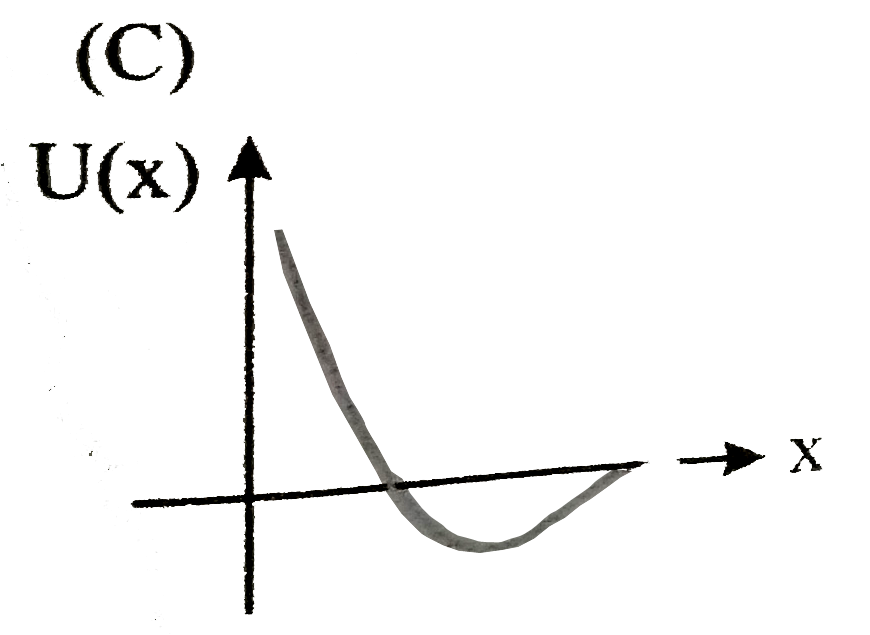 D
D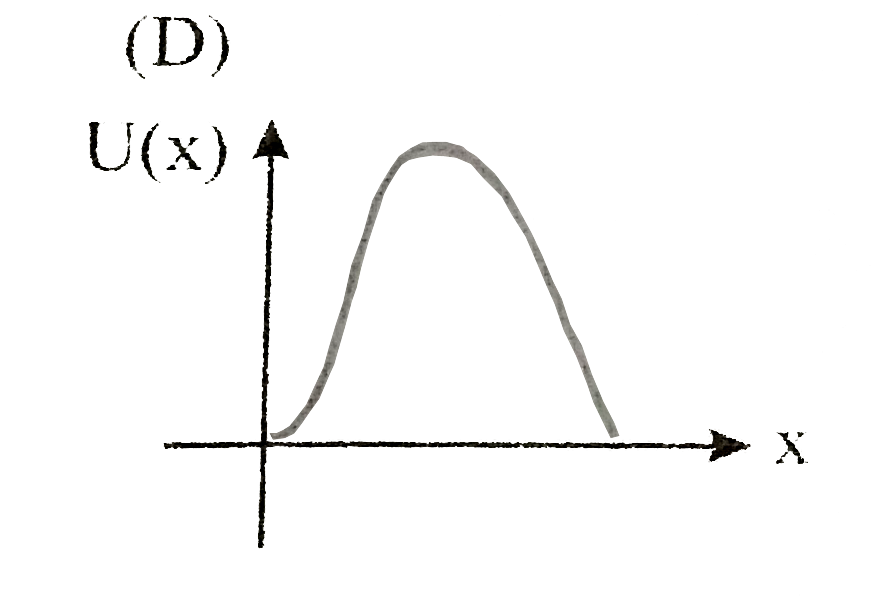
A particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants., the correct variation of potential energy function U(x) is best represented by.
View SolutionThe kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=A+x3Bx1/4+C .Write the dimensional formula for A2B
View SolutionThe kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=A+x3Bx1/4+C .Write the dimensional formula for A2B
View SolutionA particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
View SolutionA particle is projected with velocity V0along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., a=ωx2.distance at which the particle stops is
View Solution
