Find the moment of inertia of a disc of mass 3 kg and radius 50 cm about the following axes.
axis passing through the center and lying on the plane of the disc.
The moment of inertia (I) about an axis passing through the center and lying on the plane of the disc is,

where,
Topper's Solved these Questions
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES BOOK - NCERT TAMILCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES EXERCISE - EXERCISE (I. MULTI CHOICE QUESTION)
15 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES BOOK - NCERT TAMILCHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODIES EXERCISE - EXERCISE (V. NUMERICAL PROBLEMS)
6 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT TAMILCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ADDITIONAL EXERCISES
5 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - NCERT TAMILCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - EXERCISE (V. Conceptual Questions)
5 Videos
Similar Questions
Calculate the moment of inertia of a.unifprm disc of mass 0.4 kg and radius 0.1m about an axis passing through its edge and perpendicular to the plane of die disc ?
View SolutionCalculate the moment of inertia of a ring of mass 2 kg and radius 50 cm about an axis passing through its centre and perpendicular to its plane
View Solution
Knowledge Check
The moment of Inertia of an incomplete disc of mas M and radius R as shown in figure about the axis passing through the centre and perpendicular to the plane of the disc is:
 AMR22B7MR212C7MR26D5MR212
AMR22B7MR212C7MR26D5MR212The diameter of a thin circular disc of mass 2 kg is 0.2 m. Its moment of inertia about an axis passing through the edge and perpendicular to the plane of the disc is
A0.01 kg - m2B0.02 kg - m2C0.03 kg - m2D0.04 kg - m2Four similar point masses (m each) are symmetrically placed on the circumference of a disc of mass M and radius R. Moment of inertia of the system about an axis passing through centre O and perpendicular to the plane of the disc will be
AMR2+4mR2BMR2+85mR2CmR2+4MR2DMR22+4mR2
Calculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View SolutionCalculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionA uniform disc of radius R=20cm has a round cut as shown in figure. The mass of the remaining (shaded) portion of the disc equals m=7.3kg. Find the moment of inertia of such a disc relative to the axis passing through its centre of inertia and perpendicular to the plane of the disc.

View SolutionA uniform disc of radius R has a round disc of radius R/3 cut as shown in Fig. The mass of the remaining (shaded) portion of the disc equals M. Find the moment of inertia of such a disc relative to the axis passing through geometrical centre of original disc and perpendicular to the plane of the disc.
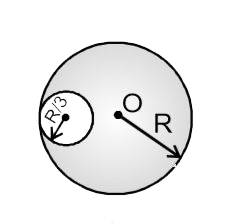
View SolutionCalculate the moment of inertia of uniform circular disc of mass 500 g, radius 10 cm about : the axis through the centre of the disc and perpendicular to its plane
View Solution
