figure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.
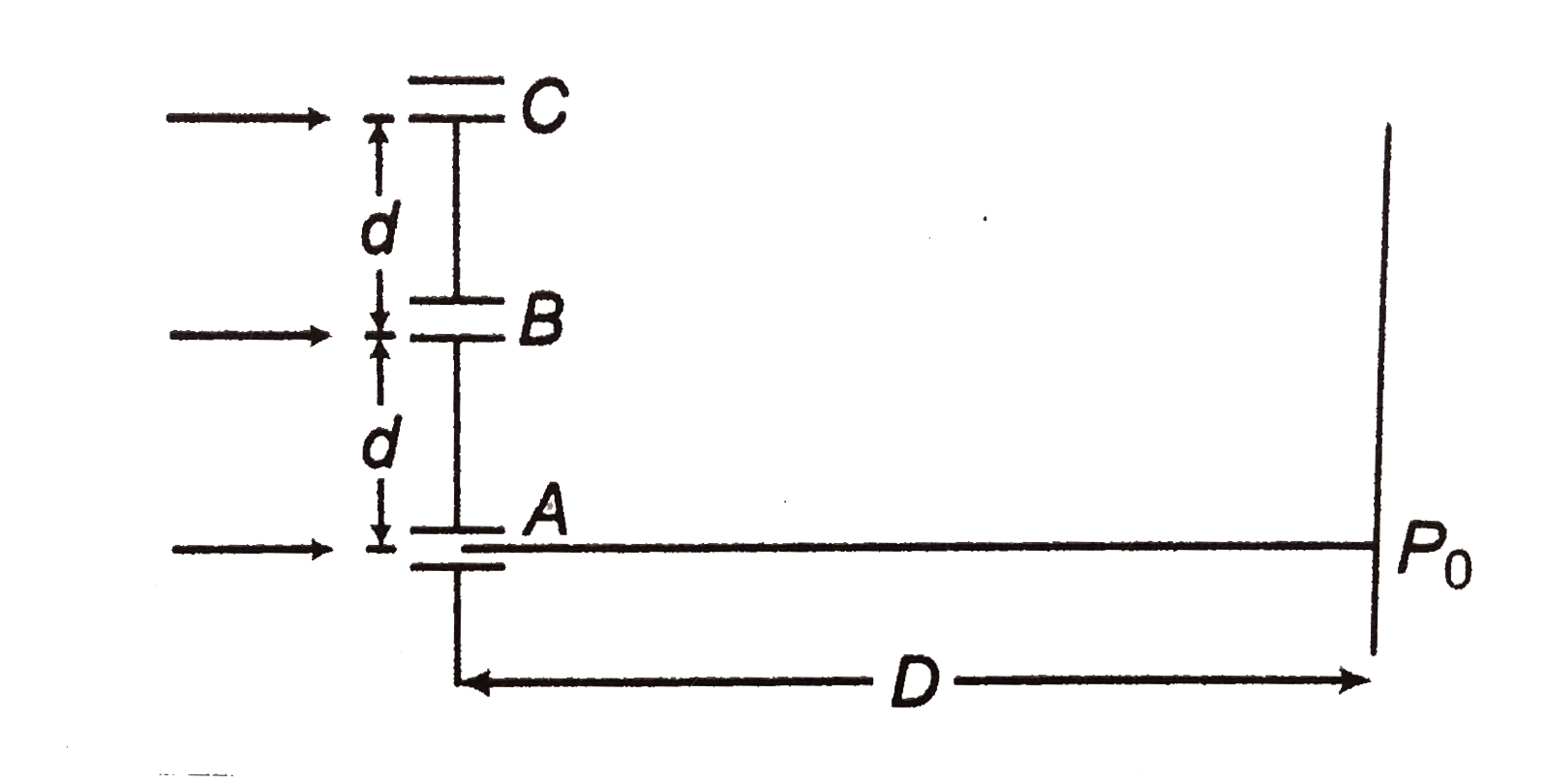
(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.Solution in Gujrati
The correct Answer is:A
a. BP−AB=13
→√D2+d2−D=λ3
→D2+d2=D2+(λ29)+2λD3
→d=θ2lamdD3
(neglecting the term λ29 as it is very small)
b. To fing the inensity at P we have to consider the inteference of light waves coming from all the three slits.
HereCP−AP−√D2+4d2−D
=√D2+8λD−D
=D{1+8λ3λ}12−D
=D{1+8λ3D×2+..}−D
=413
[usingb∈omialexpansion]<br>So, the corresponding phase difference between waves from C and A is
ϕc=2πxλ=2πx4λ3λ
=8π3=(2π+2π3)
=2π3 ..............i
Aga∈θB=2πλ3λ=2π3.......i
so it can be said that light from B and C are i same phase as they have same phase difference with respect to A.
So, R=√(2)2+r2+2×2r×rcos(2π3)
[using vector method]
=√4r2+r2+2r2.√3r
∴lp0=K(√3r2)=3Kr2=3l
As the resulting amplitude is m3 times the intensity due to individual slits.
Topper's Solved these Questions
Similar Questions
A light wave can travel
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionAn alpha particle is projected vertically upward a speed of 3.0X104kms−1 in a region where a magnetic field of magnitude 1.0 T exists in the direction south to north. Find the magnetic force that acts on the a particle.
View Solutionfigure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.

(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.
View SolutionIn Young's double slit experiment using monochromatic light of wavelength lambda , the intensity of light at a point on the screen where path diff. is lambda is K units. Find the intensity of light at a point where path difference is lambda//3 .
View SolutionShow that maximum intensity in interference pattern is four times the intensity due to each slit. Hence show that interference involves only redistribution of energy.
View SolutionThree narrow slits A, B and C are illuminated by a parallel beam of light of wavelengthλ , P is a point on the screen exactly in front of point A. Slit plane is at a distance D from the screen(D>>λ). It is know that BP – AP =13
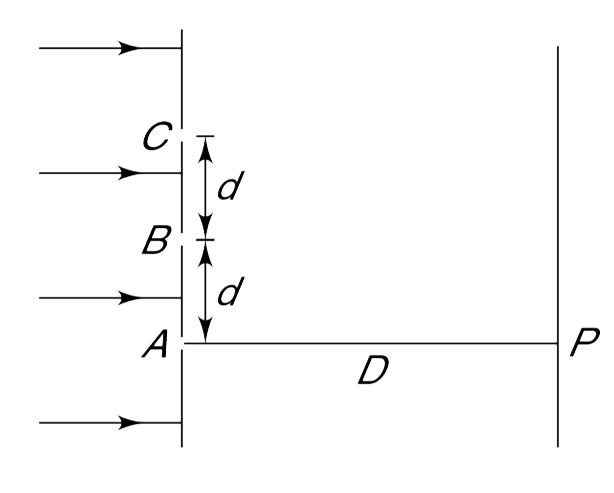
(a) Find d in terms of D andλ
(b) Write the phase difference between waves reaching at P from C and A.
(c) If intensity of P due to any of the three slits individu- ally is I0, find the resultant intensity at P.
View SolutionIn young's double slit experiment using monochromatic light of wavelengths lambda , the intensity of light at a point on the screen with path difference lambda is M units. The intensity of light at a point where path difference is lambda//3 is
View SolutionDraw a graph showing the intensity distribution of fringes due to diffraction at single slit
View Solutionएक समान्तर एकवर्णी प्रकाश पुंज से प्रकाशित एक संकीर्ण स्लिट द्वारा प्राप्त विवर्तन प्रतिरूप का वर्णन कीजिए तथा तीव्रता वितरण आरेख खींचकर इसकी व्याख्या कीजिए |
View SolutionIn a Young's double slit experiment, the separation between the two slits is d and the wavelength of the light is lambda .The intensity of light falling on slit 1 is four times the intensity of light falling on slit 2.Choose the correct choice(s).
View SolutionIn a single-slit diffraction experiment, light of wavelength λ illuminates the slit of width 'a' and the diffraction pattern is observed on a screen.
(a) Show the intensity distribution in the pattern with the angular position θ.
(b) How are the intensity and angular width of central maxima affected when
(i) width of slit is increased, and
(ii) separation between slit and screen is decreased ?
View SolutionIn Young's double-slit experiment using monochromatic light of wavelength lambda , the intensity of light at a point on the screen where path difference is lambda , is K units. What is the intensity of light at a point where path difference is lambda//3 ?
View Solutionfigure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.

(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.
View SolutionIn Young.s double-slit experiment using monochromatic light of wavelength lambda , the intensity of light at a point on the screen where path difference is lambda , is K units. What is the intensity of light at a point where path difference is lambda"/"3 ?
View SolutionIn young's double slit experiment using monochromatic light of wavelengths lambda , the intensity of light at a point on the screen with path difference lambda is M units. The intensity of light at a point where path difference is lambda//3 is
View Solution
