figure shows three equidistant slits illuminated by a monochromatic parallel beam of light. Let BP0−AP0=λ3 and D>>λ.
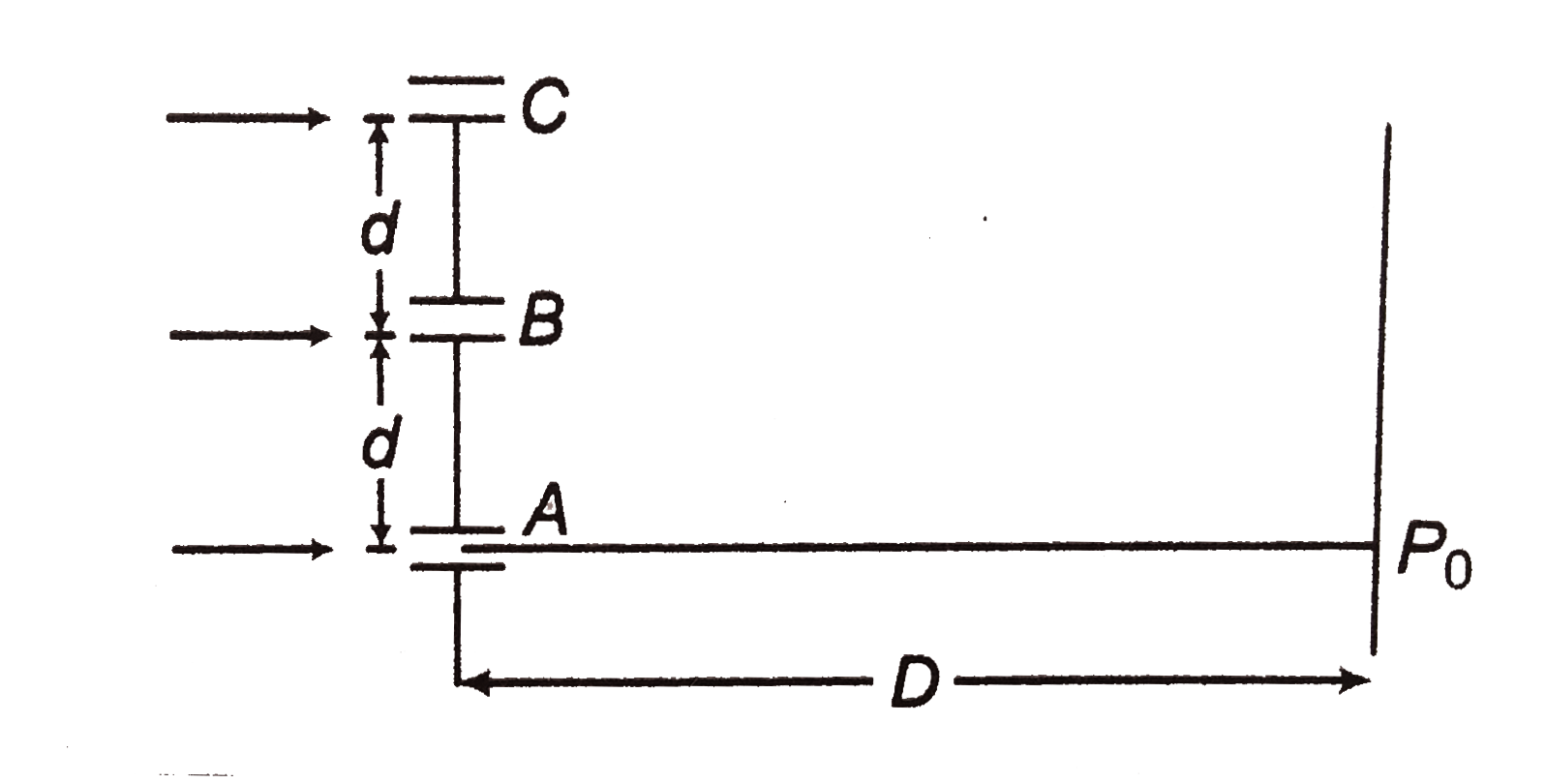
(a) Show that d = √(2λD)/3
(b) Show that the intensity at P0 is three times the intensity due to any of the three slits
individually.
The correct Answer is:A
a. BP−AB=13
→√D2+d2−D=λ3
→D2+d2=D2+(λ29)+2λD3
→d=θ2lamdD3
(neglecting the term λ29 as it is very small)
b. To fing the inensity at P we have to consider the inteference of light waves coming from all the three slits.
HereCP−AP−√D2+4d2−D
=√D2+8λD−D
=D{1+8λ3λ}12−D
=D{1+8λ3D×2+..}−D
=413
[usingb∈omialexpansion]<br>So, the corresponding phase difference between waves from C and A is
ϕc=2πxλ=2πx4λ3λ
=8π3=(2π+2π3)
=2π3 ..............i
Aga∈θB=2πλ3λ=2π3.......i
so it can be said that light from B and C are i same phase as they have same phase difference with respect to A.
So, R=√(2)2+r2+2×2r×rcos(2π3)
[using vector method]
=√4r2+r2+2r2.√3r
∴lp0=K(√3r2)=3Kr2=3l
As the resulting amplitude is m3 times the intensity due to individual slits.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -210videos
LIGHT WAVES
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective29videos
MAGNETIC FIELD
Similar Questions
Figure shows a narrow slit S illuminated b a monochromatic light of wavelength λ in a double-slit experiment. In the path of the rays reaching the upper slit S1, a tube to length L is interposed in which the index of reflection of the medium varies linearly as shown in figure . The position of the central maximum in the interference pattern on the screen was displaceed by N fringes. Find the value of N in terms of μ0, L and λ.
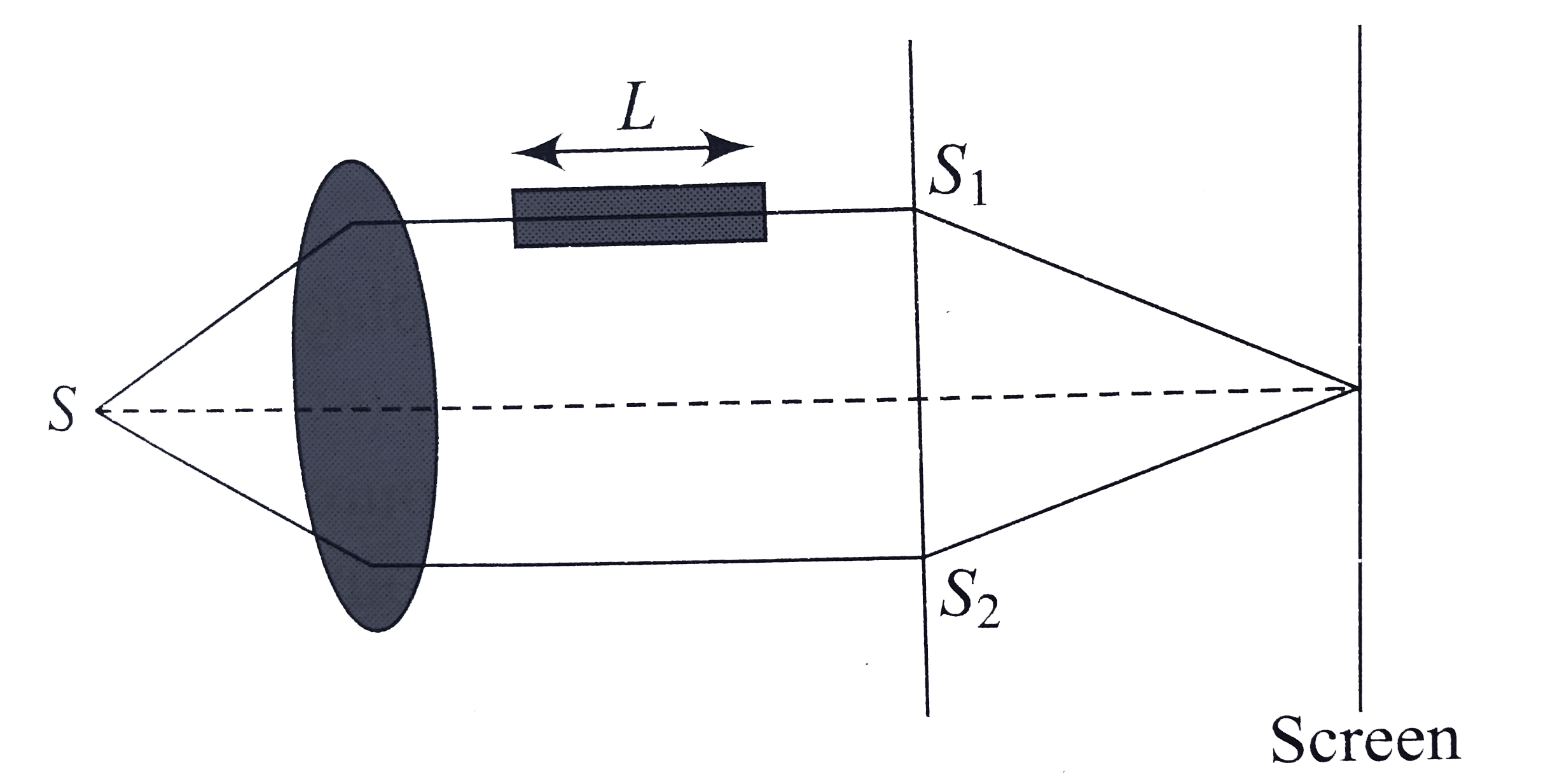
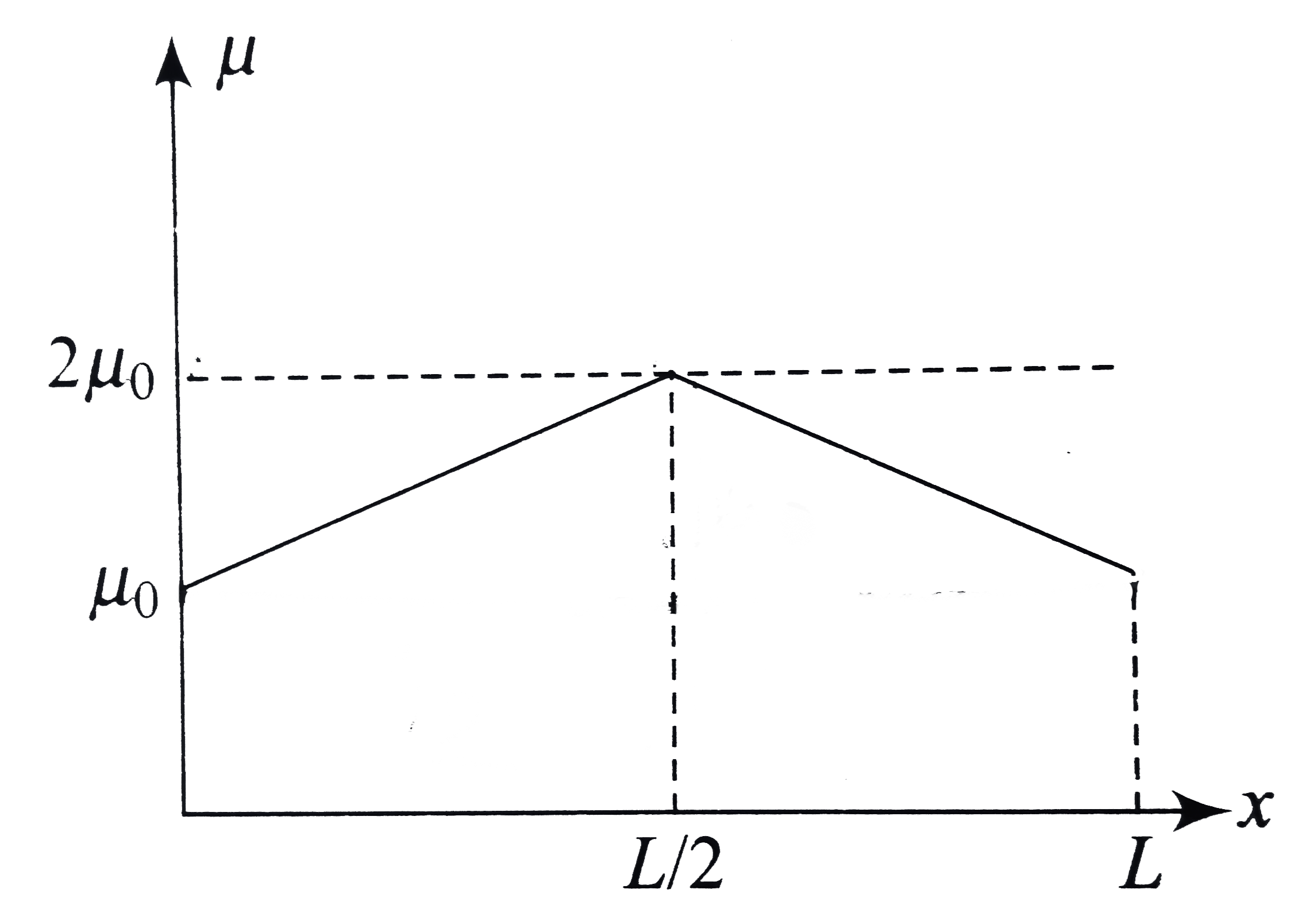 View Solution
View Solution_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-View SolutionA Young's double slit experiment uses a monochromatic light of wavelength λ. The intensity of each slit is same and is equal to I0. What will be the resultant intensity at a point where waves interfere at a path difference of λ2 ?
View SolutionIn the figure shown three slits s1,s2 and s3 are illuminated with of wavelength λ.λ<<d and D>>d. Each slit prouduces same intensity I on the screen. If intensity at the point on screen directly infront of s2 is 3I then the maximum value of λ is nd22D Find value of n.
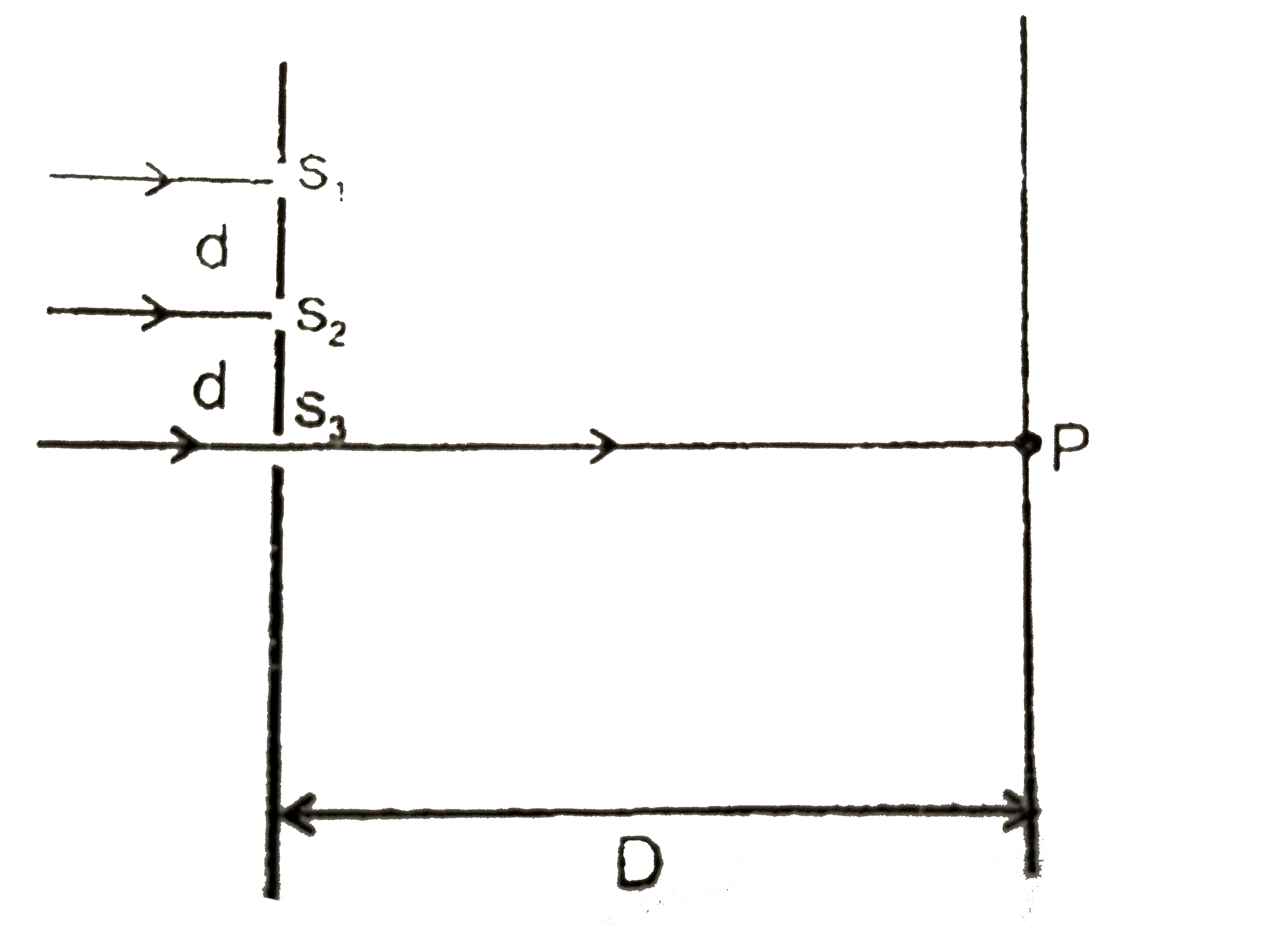 View Solution
View SolutionIn a Young's double slit set up using monochromatic light of wavelength λ the intensity of light at a point, where path difference is 2λ is found to be I0 What will be the intensity at a point when path different is λ/3 ?
View SolutionConsider the situation shown in figure. The two slits S1andS2 placed symmetrically around the central line are illuminated by a monochromatic light of wavelength λ. The separation between the slits is d. The light transmitted by the slits falls on a screen Σ1 placed at a distance D from the slits. The slit S3 is at the placed central line and the slit S4, is at a distance z from S3. Another screenΣ2 is placed a further distance D away from 1,1. Find the ratio of the maximum to minimum intensity observed on Σ2 if z is equal to a. z=λD2d b. λDd c. λD4d
 View Solution
View SolutionConsider the situation shown in figure. The two slite S1andS2
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen M1 placed at a distance D from the slits. The slit S3 is
at the centre line and the slit S4 is at a distance y form S3. Another screen M2 is
placed at a further distance D away from M1. Find the ration of the maximum to
minimum intensity observed on M2 if y is equal to (d<<D).
View SolutionTwo coherent narrow slits emitting light of wavelength λ in the same phase are placed parallel to each other at a small separation of 2λ. The light is collected on a screen S which is placed at a distance D(gtgtλ) from the slit S1 as shown in figure. Find the finite distance x such that the intensity at P is equal to intensity O.
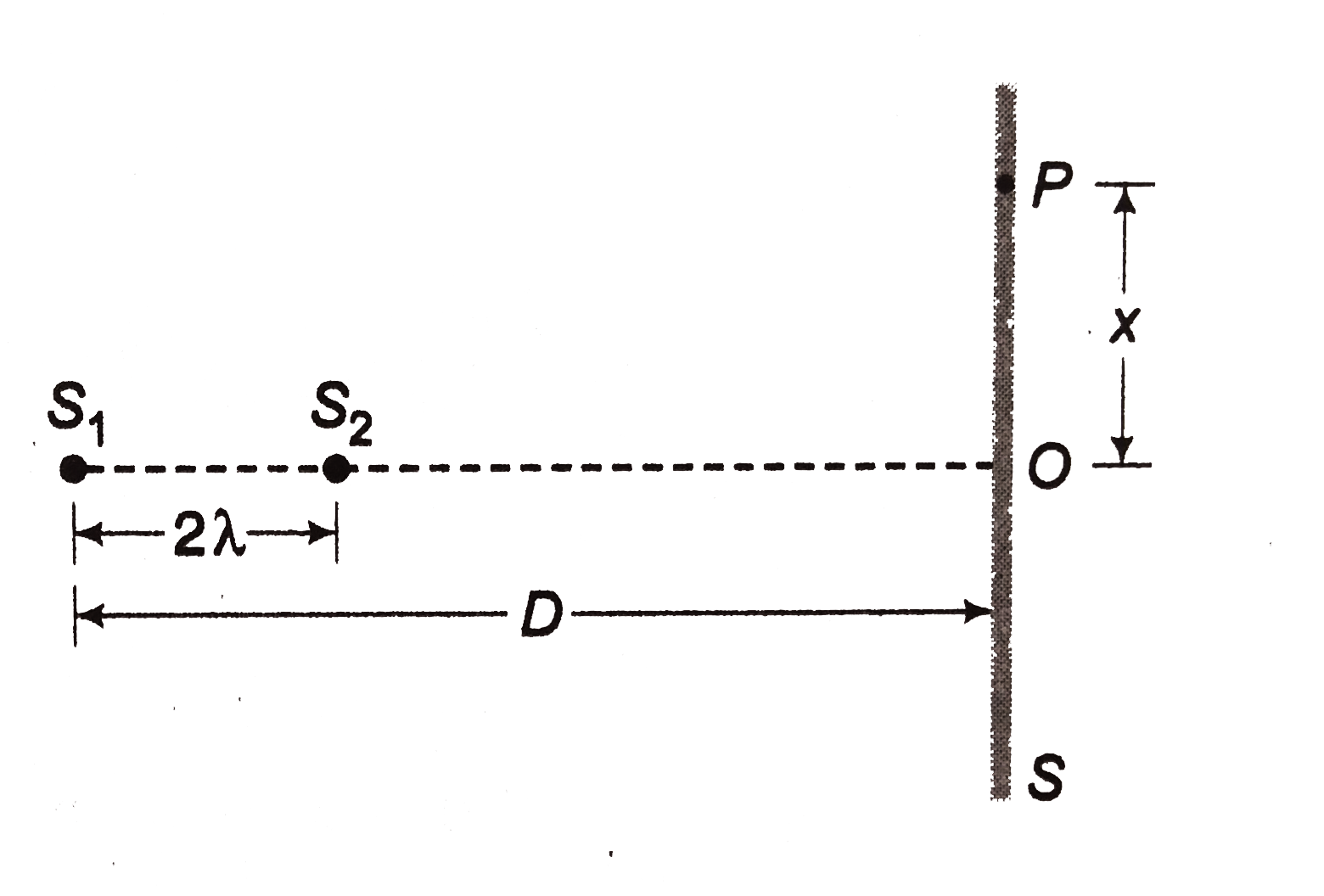 .View Solution
.View SolutionShow that the three straight lines 2x−3y+5=0,3x+4y−7=0and9x−5y+8=0 meet in a point
View SolutionShow that the points A(2,1),B(0,3),C(−2,1)andD(0,−1) are the vertices of a square.
View Solution

